T geçitleri ve T fabrikaları

Bu makalede, hataya dayanıklı kuantum bilişiminde T geçitlerinin ve T fabrikalarının rolü açıklanmaktadır. Bir kuantum algoritması vererek, T geçitlerini ve T fabrikalarını çalıştırmak için gerekli kaynakların tahmini önemli hale gelir.

Kuantum geçitlerinin evrensel kümesi

DiVincenzo'nun ölçütlerine göre ölçeklenebilir bir kuantum bilgisayarın evrensel bir kuantum kapısı kümesi uygulayabilmesi gerekir. Evrensel küme, herhangi bir kuantum hesaplaması gerçekleştirmek için gereken tüm geçitleri içerir; diğer bir ifadeyle, herhangi bir hesaplamanın evrensel geçitlerden oluşan sonlu bir diziye geri ayrıştırılması gerekir. En azından, kuantum bilgisayarın tek kubitleri Bloch Sphere üzerindeki herhangi bir konuma taşıyabilmesi (tek kubitli geçitler kullanarak) ve sistemde çok kubitli bir kapı gerektiren dolanıklık oluşturabilmesi gerekir.

Klasik bilgisayarda bir bit ile bir bit arasında eşleyen yalnızca dört işlev vardır. Buna karşılık, kuantum bilgisayardaki tek bir kubitte sonsuz sayıda birimsel dönüşüm vardır. Bu nedenle, hiçbir sonlu temel kuantum işlemi veya geçidi kümesi, kuantum bilişiminde izin verilen sonsuz birimsel dönüşüm kümesini tam olarak çoğaltabilir. Bu, klasik bilgi işlemden farklı olarak bir kuantum bilgisayarın mümkün olan her kuantum programını tam olarak sınırlı sayıda geçit kullanarak uygulaması mümkün olmadığı anlamına gelir. Bu nedenle kuantum bilgisayarlar, klasik bilgisayarlarla aynı anlamda evrensel olamaz. Sonuç olarak, kuantum bilişimi için bir dizi geçidin evrensel olduğunu söylediğimizde, klasik bilgi işlemden biraz daha zayıf bir anlama geliriz.

Evrensellik için, kuantum bilgisayarın sonlu uzunluklu bir geçit dizisi kullanarak yalnızca sonlu bir hata içindeki her birim matrise yakın olması gerekir.

Başka bir deyişle, herhangi bir birim dönüştürme yaklaşık olarak bu kümedeki kapıların bir ürünü olarak yazılabilirse, bir kapı kümesi evrensel bir kapı kümesidir. Önceden belirlenmiş herhangi bir hata sınırı için kapı kümesinden G_, G_{1}{2}, \ldots G_N$ geçitleri olması $gerekir.

$${G_N G_N-1}\cdots G_2 G_1 \approx U.$$

Matris çarpma kuralı sağdan sola doğru bu dizideki ilk geçit işlemini çarpmak olduğundan G_N$$, kuantum durumu vektörine uygulanan son işlemdir. Daha resmi olarak, her hata toleransı $\epsilon>0 $$ için G_1, \ldots G_N G_N\ldots G_1$$ ve $U$ arasındaki $uzaklık en fazla $\epsilon olacak şekilde varsa, böyle bir kapı kümesinin$ evrensel olduğu söylenir. İdeal olarak bu \epsilon uzaklığı $ulaşmak için gereken N$ değeri$, 1/\epsilon$$ ile $poli-logaritmik olarak ölçeklendirilmelidir.

Örneğin, Hadamard, CNOT ve T geçitleri tarafından oluşturulan küme, herhangi bir kuantum hesaplamasının (herhangi bir sayıda kubit üzerinde) oluşturulabileceği evrensel bir kümedir. Hadamard ve T kapısı kümesi herhangi bir tek kubitli kapı oluşturur:

$$H=\frac{1}{\sqrt{ 1 amp; 1 \\ 1 &-1 \end{bmatrix}, \qquad T=\begin{bmatrix} 1 & 0 \\ 0 & e^{i\pi/4}\end{bmatrix}.&{2}}\begin{bmatrix} $$

Kuantum bilgisayarda kuantum geçitleri iki kategoriye ayrılır: Clifford geçitleri ve Clifford olmayan kapılar, bu örnekte T kapısı. Yalnızca Clifford geçitlerinden yapılan kuantum programları, klasik bir bilgisayar kullanılarak verimli bir şekilde benzetilebilir ve bu nedenle kuantum avantajı elde etmek için Clifford olmayan geçitler gerekir. Birçok kuantum hata düzeltmesi (QEC) şemasında Clifford geçitlerinin uygulanması kolaydır, yani hataya dayanıklı bir şekilde uygulamak için işlemler ve kubitler açısından çok az kaynak gerektirirken, Clifford olmayan kapılar hataya dayanıklılık gerektirdiğinde oldukça maliyetlidir. Evrensel kuantum kapısı kümesinde, T kapısı yaygın olarak Clifford olmayan kapı olarak kullanılır.

içinde varsayılan olarak Q#dahil edilen tek kubitli Clifford geçitlerinin standart kümesi dahil

$$H=\frac{{1}{\sqrt{{2}}\begin{bmatrix} 1 & 1 1 &\\ amp;-1 \end{bmatrix} , \qquad S =\begin{bmatrix} 1 & 0 \\ 0 & i \end{bmatrix}= T^2, \qquad X=\begin{bmatrix} 0 & 1 \\ 1& 0 \end{bmatrix}= HT^4H,$$

$$ Y =\begin{bmatrix} 0 & -i \\ i & 0 \end{bmatrix}=T^2HT^4 HT^6, \qquad Z=\begin{bmatrix}1& 0\\ 0&&-1 \end{bmatrix}=T^4. $$

Clifford olmayan kapı (T kapısı) ile birlikte, bu işlemler tek bir kubit üzerindeki herhangi bir birim dönüşümü yaklaşık olarak oluşturmak için oluşturulabilir.

Azure Quantum Kaynak Tahmin Aracı'ndaki T fabrikaları

Diğer kuantum geçitleri evrensel kuantum hesaplaması için yeterli olmadığından Clifford olmayan T kapısı hazırlığı çok önemlidir. Pratik ölçekli algoritmalar için Clifford dışı işlemleri uygulamak için düşük hata oranı T geçitleri (veya T durumları) gerekir. Ancak, mantıksal kubitler üzerinde doğrudan uygulanması zor olabilir ve bazı fiziksel kubitler için de zor olabilir.

Hataya dayanıklı bir kuantum bilgisayarda, gerekli düşük hata oranına sahip T durumları bir T durumu damıtma fabrikası veya kısaca T fabrikası kullanılarak üretilir. Bu T fabrikaları genellikle bir dizi damıtma işlemi içerir; burada her tur daha küçük bir mesafe koduyla kodlanmış çok sayıda gürültülü T durumu alır, bunları bir damıtma birimi kullanarak işler ve daha büyük bir mesafe kodunda kodlanmış daha az gürültülü T durumu çıkarır ve yuvarlama sayısı, damıtma birimleri ve uzaklıkların tümünün parametre olması değiştirilebilir. Bu yordam yinelenir ve burada bir turun çıkış T durumları giriş olarak bir sonraki tura aktarılır.

T fabrikasının süresine bağlı olarak , Azure Quantum Kaynak Tahmin Aracı bir T fabrikasının algoritmanın toplam çalışma zamanını aşmadan önce ne sıklıkta çağrılabileceğini ve dolayısıyla algoritma çalışma zamanı sırasında kaç T durumunun üretilebileceğini belirler. Genellikle algoritma çalışma zamanı sırasında tek bir T fabrikasının çağrılarında üretilebilenden daha fazla T durumu gerekir. Kaynak Tahmin Aracı, daha fazla T durumu üretmek için T fabrikalarının kopyalarını kullanır.

T fabrika fiziksel tahmini

Kaynak Tahmin Aracı, algoritmayı çalıştırmak için gereken toplam T durumu sayısını ve tek bir T fabrikası ile çalışma zamanı için fiziksel kubit sayısını hesaplar.

Amaç, algoritma çalışma zamanı içindeki tüm T durumlarını mümkün olduğunca az T fabrika kopyasıyla üretmektir. Aşağıdaki diyagramda algoritmanın çalışma zamanı ve bir T fabrikasının çalışma zamanı örneği gösterilmektedir. T fabrikasının çalışma zamanının algoritmanın çalışma zamanından daha kısa olduğunu görebilirsiniz. Bu örnekte, bir T fabrikası bir T durumunu damıtabilir. İki soru ortaya çıkar:

• T fabrikası algoritmanın sonundan önce ne sıklıkta çağrılabilir?
• Algoritmanın çalışma zamanı sırasında gereken T durumlarının sayısını oluşturmak için T fabrika damıtma turunun kaç kopyası gereklidir?

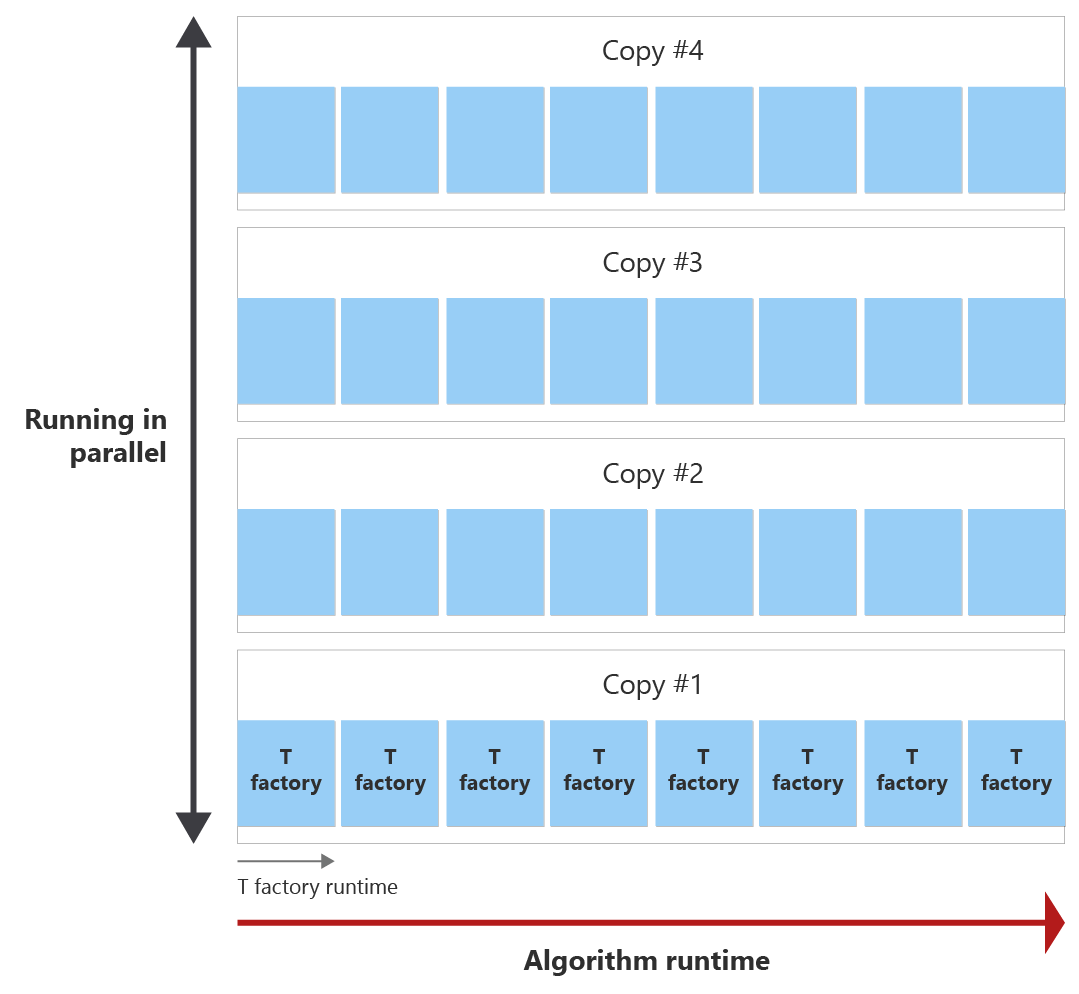
Algoritma bitmeden önce, T fabrikası sekiz kez çağrılabilir ve bu da damıtma yuvarlakı olarak adlandırılır. Örneğin, 30 T durumu gerekiyorsa, algoritmanın çalışma zamanı sırasında tek bir T fabrikası sekiz kez çağrılır ve bu nedenle sekiz T durumu oluşturur. Ardından, gereken 30 T durumlarını damıtmak için paralel olarak çalışan T fabrika damıtma turunun dört kopyasına ihtiyacınız vardır.

Not

T fabrika kopyalarının ve T fabrika çağrılarının aynı olmadığını unutmayın.

T durumu damıtma fabrikaları, her yuvarlamanın paralel çalışan damıtma birimlerinin bir dizi kopyasından oluştuğu bir dizi yuvarlamada uygulanır. Kaynak Tahmin Aracı, bir T fabrikasını çalıştırmak için kaç fiziksel kubit gerektiğini ve T fabrikasının ne kadar süreyle çalıştığını ve diğer gerekli parametreleri hesaplar.

Yalnızca bir T fabrikasının tam çağrılarını yapabilirsiniz. Bu nedenle, tüm T fabrika çağrılarının birikmiş çalışma zamanının algoritma çalışma zamanından küçük olduğu durumlar olabilir. Kubitler farklı yuvarlamalar tarafından yeniden kullanıldığından, bir T fabrikası için fiziksel kubit sayısı, bir tur için kullanılan en fazla fiziksel kubit sayısıdır. T fabrikasının çalışma zamanı, tüm yuvarlamalardaki çalışma zamanının toplamıdır.

Not

Fiziksel T kapısı hata oranı gerekli mantıksal T durumu hata hızından düşükse, Kaynak Tahmin Aracı iyi bir kaynak tahmini gerçekleştiremez. Bir kaynak tahmini işi gönderdiğinizde, gerekli mantıksal T durumu hata oranı çok düşük veya çok yüksek olduğundan T fabrikasının bulunamamasıyla karşılaşabilirsiniz.

Daha fazla bilgi için bkz. Pratik kuantum avantajına ölçeklendirmek için gereksinimleri değerlendirmeye ilişkin Ek C.

Sonraki adımlar

• Hisse devreleri
• Kuantum oracle’ları
• Grover algoritması
• Kuantum Ara Gösterimi