你当前正在访问 Microsoft Azure Global Edition 技术文档网站。 如果需要访问由世纪互联运营的 Microsoft Azure 中国技术文档网站,请访问 https://docs.azure.cn。
本教程介绍如何编写一个基本量子程序 Q# ,以利用量子力学的性质生成随机数。
在本教程中,将:
- 创建 Q# 程序。
- 查看程序的主要组件 Q# 。
- 定义问题的逻辑。
- 将经典操作和量子操作相结合来解决问题。
- 使用量子位和叠加来生成量子随机数生成器。
提示
若要加速量子计算之旅,请查看 Azure Quantum 代码,这是 Microsoft Quantum 网站的独特功能。 在这里,你可以运行内置 Q# 示例或你自己的 Q# 程序,通过提示生成新 Q# 代码,在 VS Code for Web 中打开并运行代码,只需单击一下,并询问有关量子计算的 Copilot 问题。
先决条件
若要在 Azure Quantum 的 Copilot 中运行代码示例,
- Microsoft(MSA)电子邮件帐户。
若要在 Visual Studio Code 中开发和运行代码示例,请执行以下操作:
最新版本的 Visual Studio Code 或打开网页版 VS Code。
最新版本的 Azure Quantum Development Kit 扩展。 有关安装详细信息,请参阅 设置 QDK 扩展。
如果要使用 Jupyter Notebook,则还需要安装 Python 和 Jupyter 扩展,以及具有额外功能的最新
qdkPython 库jupyter。 为此,请打开终端并运行以下命令:pip install --upgrade qdk[jupyter]
定义问题
经典计算机不会生成随机数,而是生成伪随机数。 伪随机数生成器基于一些初始值(称为种子)生成确定性数字序列。 为了更好地估计随机值,此种子通常是 CPU 时钟的当前时间。
另一方面,量子计算机可以生成真正的随机数。 这是因为叠加量子比特的测量是一个概率过程。 测量结果是随机的,无法预测结果。 这是量子随机数生成器的基本原理。
量子比特是可以叠加的量子信息的单位。 测量时,量子位只能处于 0 状态或处于 1 状态。 但是,在测量之前,量子比特的状态表示使用度量读取 0 或 1 的概率。
从处于基态(例如 0)的量子比特入手。 随机数生成器的第一步是使用 Hadamard 运算将量子比特置于等概率叠加态。 此状态的度量结果为 0 或 50% 概率为 50% 的结果,这是一个真正的随机位。
在叠加中测量量子位后,无法知道将得到什么,每次调用代码时,结果都是不同的值。 但如何才能通过这种行为生成更大的随机数?
假设重复这个过程四次,生成以下二进制数字序列:
$${0、1、1、0}$$
如果将这些位连接或合并成一个位字符串,就可以形成更大的数字。 在此示例中,位序列 ${0110}$ 等同于十进制的 6。
$${0110_{\ binary} \equiv 6_{\ decimal}}$$
如果多次重复执行此过程,则可以将多个比特组合成任何一个大数字。 使用此方法,可以创建一个数字来用作安全密码,因为可以确保没有黑客可以确定度量序列的结果。
定义随机数生成器逻辑
让我们概述随机数生成器的逻辑应是什么:
- 将
max定义为要生成的最大数字。 - 定义需要生成的随机比特的数目。 这是通过计算位数来完成的,
nBits你需要将整数表示为最多max。 - 生成长度为
nBits的随机位字符串。 - 如果位字符串表示一个大于
max的数,则返回到步骤 3。 - 否则,此过程完成。 返回生成的数字(整数形式)。
例如,我们将 max 设置为 12。 也就是说,12 是要用作密码的最大数字。
需要 ${\lfloor ln(12) / ln(2) + 1 \rfloor}$ 或 4 比特来表示一个介于 0 和 12 之间的数字。 可以使用内置函数,该函数 BitSizeI采用任何整数并返回表示它所需的位数。
假设生成了位字符串 ${1101_{\ binary}}$,它等同于 ${13_{\ decimal}}$。 由于 13 大于 12,因此将复该过程。
接下来,生成位字符串 ${0110_{\ binary}}$,它等同于 ${6_{\ decimal}}$。 由于 6 小于 12,因此该过程完成。
量子随机数生成器将返回数字 6 作为密码。 在实际操作中,将较大的数字设置为最大数字,因为较小的数字很容易通过尝试所有可能的密码而被破解。 实际上,为了增加猜测或破解密码的难度,可以使用 ASCII 代码将二进制数转换为文本,并使用数字、符号和混合大小写的字母生成密码。
编写随机位生成器
第一步是编写生成 Q# 随机位的操作。 此操作将是随机数生成器的构建基块之一。
operation GenerateRandomBit() : Result {
// Allocate a qubit.
use q = Qubit();
// Set the qubit into superposition of 0 and 1 using the Hadamard
H(q);
// At this point the qubit `q` has 50% chance of being measured in the
// |0〉 state and 50% chance of being measured in the |1〉 state.
// Measure the qubit value using the `M` operation, and store the
// measurement value in the `result` variable.
let result = M(q);
// Reset qubit to the |0〉 state.
// Qubits must be in the |0〉 state by the time they are released.
Reset(q);
// Return the result of the measurement.
return result;
}
现在来看看新代码。
- 定义
GenerateRandomBit运算,它不接受输入,并生成Result类型的值。Result类型表示测量的结果,可能为以下任一值:Zero或One。 - 使用关键字分配单个量子比特
use。 分配时,量子位始终处于 |0} 状态。 - 使用该
H操作将量子位置于相等叠加中。 - 使用
M运算测量量子比特,返回度量值(Zero或One)。 - 使用
Reset操作将量子比特重置为 |0} 状态。
通过 H 操作将量子比特置于叠加态并通过 M 操作对其进行测量以后,每次调用代码时,结果都会是一个不同值。
Q#使用 Bloch 球可视化代码
在 Bloch 球体中,北极表示经典值 0,南极表示经典值 1。 任何叠加态都可以用球上的某个点来表示(用箭头表示)。 箭头末端越靠近极点,量子位塌缩成经典值(在度量时分配给该极点)的概率越高。 例如,以下图中箭头表示的量子位状态,如果对其进行测量,它给出的值更有可能是 0。

你可以使用此表示法将代码的功能可视化:
首先,从以 |0〉 状态初始化的量子比特开始,并应用一个
H操作,来创建一个相等的叠加态,其中 0 和 1 的概率相同。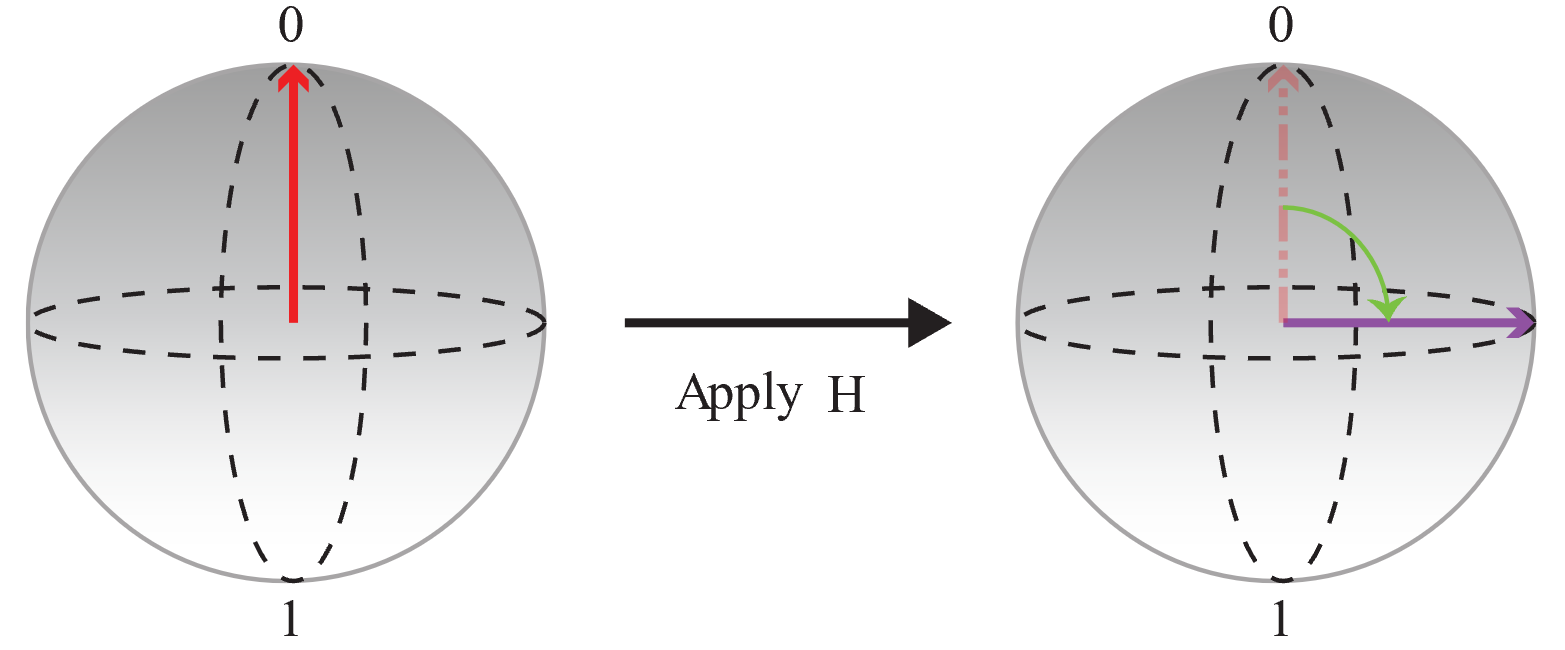
然后,测量该量子比特并保存输出:

由于度量结果是随机的,并且测量 0 和 1 的概率是相同的,因此你获得了完全随机的位。 可以多次调用此操作来创建整数。 例如,如果调用此操作三次来获取三个随机位,就可以生成随机的 3 位数(即 0 到 7 之间的随机数)。
编写完整的随机数生成器
首先,需要将所需的命名空间从 Q# 标准库导入到程序。 编译器 Q# 会自动加载许多常见函数和操作,但是对于完整的随机数生成器,需要两 Q# 个命名空间中的一些附加函数和操作:
Std.Math以及Std.Convert。import Std.Convert.*; import Std.Math.*;接下来,定义
GenerateRandomNumberInRange操作。 此操作重复调用GenerateRandomBit操作以生成位字符串。/// Generates a random number between 0 and `max`. operation GenerateRandomNumberInRange(max : Int) : Int { // Determine the number of bits needed to represent `max` and store it // in the `nBits` variable. Then generate `nBits` random bits which will // represent the generated random number. mutable bits = []; let nBits = BitSizeI(max); for idxBit in 1..nBits { bits += [GenerateRandomBit()]; } let sample = ResultArrayAsInt(bits); // Return random number if it is within the requested range. // Generate it again if it is outside the range. return sample > max ? GenerateRandomNumberInRange(max) | sample; }让我们花点时间回顾一下新代码。
- 你需要计算表示最大为
max的整数所需的位数。 命名空间BitSizeI中的Std.Math函数将整数转换为表示它所需的位数。 -
SampleRandomNumberInRange操作使用for循环来生成随机数,直到生成的数字等于或小于max为止。for循环的工作方式与其他编程语言中的for循环完全相同。 - 变量
bits是可变变量。 可变变量是计算过程中可以更改的变量。 使用set指令可以更改可变变量的值。 - 该
ResultArrayAsInt函数从默认Std.Convert命名空间将位字符串转换为正整数。
- 你需要计算表示最大为
最后,将入口点添加到程序。 默认情况下, Q# 编译器会查找操作
Main并开始处理。 它调用GenerateRandomNumberInRange该操作以生成介于 0 和 100 之间的随机数。operation Main() : Int { let max = 100; Message($"Sampling a random number between 0 and {max}: "); // Generate random number in the 0..max range. return GenerateRandomNumberInRange(max); }let指令声明在计算过程中不更改的变量。 此处将最大值定义为 100。有关操作的详细信息
Main,请参阅 入口点。随机数生成器的完整代码如下所示:
import Std.Convert.*;
import Std.Math.*;
operation Main() : Int {
let max = 100;
Message($"Sampling a random number between 0 and {max}: ");
// Generate random number in the 0..max range.
return GenerateRandomNumberInRange(max);
}
/// Generates a random number between 0 and `max`.
operation GenerateRandomNumberInRange(max : Int) : Int {
// Determine the number of bits needed to represent `max` and store it
// in the `nBits` variable. Then generate `nBits` random bits which will
// represent the generated random number.
mutable bits = [];
let nBits = BitSizeI(max);
for idxBit in 1..nBits {
bits += [GenerateRandomBit()];
}
let sample = ResultArrayAsInt(bits);
// Return random number if it is within the requested range.
// Generate it again if it is outside the range.
return sample > max ? GenerateRandomNumberInRange(max) | sample;
}
operation GenerateRandomBit() : Result {
// Allocate a qubit.
use q = Qubit();
// Set the qubit into superposition of 0 and 1 using a Hadamard operation
H(q);
// At this point the qubit `q` has 50% chance of being measured in the
// |0〉 state and 50% chance of being measured in the |1〉 state.
// Measure the qubit value using the `M` operation, and store the
// measurement value in the `result` variable.
let result = M(q);
// Reset qubit to the |0〉 state.
// Qubits must be in the |0〉 state by the time they are released.
Reset(q);
// Return the result of the measurement.
return result;
}
运行随机数生成器程序
可以在 Azure Quantum 中的 Copilot 和 Visual Studio Code 中作为独立Q#应用程序或使用 Python 主机程序运行该程序。
可以使用 Azure Quantum 中的 Copilot 免费测试 Q# 代码 - 只需Microsoft(MSA)电子邮件帐户即可。 有关 Azure Quantum 中的 Copilot 的详细信息,请参阅 探索 Azure Quantum。
在浏览器中打开 Azure Quantum 中的 Copilot。
将以下代码复制并粘贴到代码编辑器中。
import Std.Convert.*; import Std.Math.*; operation Main() : Int { let max = 100; Message($"Sampling a random number between 0 and {max}: "); // Generate random number in the 0..max range. return GenerateRandomNumberInRange(max); } /// # Summary /// Generates a random number between 0 and `max`. operation GenerateRandomNumberInRange(max : Int) : Int { // Determine the number of bits needed to represent `max` and store it // in the `nBits` variable. Then generate `nBits` random bits which will // represent the generated random number. mutable bits = []; let nBits = BitSizeI(max); for idxBit in 1..nBits { bits += [GenerateRandomBit()]; } let sample = ResultArrayAsInt(bits); // Return random number if it is within the requested range. // Generate it again if it is outside the range. return sample > max ? GenerateRandomNumberInRange(max) | sample; } /// # Summary /// Generates a random bit. operation GenerateRandomBit() : Result { // Allocate a qubit. use q = Qubit(); // Set the qubit into superposition of 0 and 1 using the Hadamard // operation `H`. H(q); // At this point the qubit `q` has 50% chance of being measured in the // |0〉 state and 50% chance of being measured in the |1〉 state. // Measure the qubit value using the `M` operation, and store the // measurement value in the `result` variable. let result = M(q); // Reset qubit to the |0〉 state. // Qubits must be in the |0〉 state by the time they are released. Reset(q); // Return the result of the measurement. return result; // Note that Qubit `q` is automatically released at the end of the block. }选择要运行的镜头数,然后选择“ 运行”。
结果显示在直方图和 结果 字段中。
选择 “解释代码 ”以提示 Copilot 向你解释代码。
提示
在 Azure Quantum 中的 Copilot 中,可以通过选择代码编辑器右侧角的 VS Code 徽标按钮,在 VS Code for Web 中打开程序。
注意
此代码片段当前未在任何可用的 Azure Quantum 硬件 targets上运行,因为可调用方 ResultArrayAsInt 需要具有 完整计算配置文件的 QPU。
相关内容
浏览其他 Q# 教程:
- 量子纠缠 演示如何编写一个 Q# 程序来操作和测量量子比特,并演示叠加和纠缠的影响。
- Grover 的搜索算法 演示如何编写 Q# 使用 Grover 搜索算法的程序。
- Quantum Fourier 转换 探索了如何编写 Q# 直接处理特定量子比特的程序。
- Quantum Katas 是自我节奏的教程和编程练习,旨在同时教授量子计算和Q#编程的元素。



