正如位元是傳統運算中的基礎資訊物件,Q 位元 (量子位元) 則是量子運算的基礎資訊物件。 為了瞭解此對應,本文將探討最簡單的範例:單一量子位。
表示量子位
雖然一位元或二進位數位可以有$0$ 或$ 1$ 的值,但量子位元可以有值為 $0$、$1$ 或是 $0$ 和 $1$ 的量子疊加。
單一量子位的狀態可由單位範數的二維數據列向量來描述,也就是說,其元素的大小平方必須加總到 $1$。 這個向量稱為量子狀態向量,會保存描述單一量子位元量子系統所需的所有資訊,就像單一位元保存描述二進位變數狀態所需的所有資訊一樣。 如需量子運算中向量和矩陣的基本概念,請參閱 向量和矩陣。
任何實數或複數的二維列向量,其範數為$1$,都代表量子位可能持有的量子狀態。 因此,如果 $\alpha$ 和 $\beta$ 是滿足 $|\alpha|^2 + |\beta|^2 = 1 的複數,則$\begin{bmatrix}\alpha\\\beta\end{bmatrix}$表示量子位狀態。$
代表量子位的有效量子狀態向量範例 $\begin{bmatrix} 1 \\ 0 \end{bmatrix}$,$\begin{bmatrix} 0 \\ 1 \end{bmatrix}$。 這兩個向量會形成描述量子位狀態的向量空間基礎。 這表示任何量子狀態向量都可以撰寫為這些基礎向量的總和。 具體而言,向量 $\begin{bmatrix} x y \\ 可以寫入為 \end{bmatrix}$x $\begin{bmatrix} 1 \\ 0 \end{bmatrix} + y \begin{bmatrix} 0 \\ 1 \end{bmatrix}$。 雖然任何這些向量的旋轉都可以作為量子位的完全有效基底,但這個特定的基底選為「計算基底」。
這兩個量子狀態用來對應經典位元的兩個狀態,即 $0$ 和 $1$。 標準慣例是選擇
$$0\equiv\begin{bmatrix} 1 \\ 0 \end{bmatrix}$$$$1 \equiv\begin{bmatrix} 0 \\ 1 \end{bmatrix},$$
雖然選擇相反的也同樣具有可行性。 因此,在可能的單量子位元量子狀態向量的無限數目中,只有兩個對應於經典位元的狀態;其他量子狀態皆不符合。
測量量子位
如何說明量子位,可以藉由討論測量概念來取得這些狀態所代表的一些直覺。 測量相當於「查看」量子位的非正式概念,其會立即將量子狀態折疊為兩個傳統狀態 $\begin{bmatrix} 1 \\ 0 \end{bmatrix}$ 或 $\begin{bmatrix} 0 \\ 1 \end{bmatrix}$的其中一個。 測量量子狀態向量$\begin{bmatrix}\alpha\\\beta\end{bmatrix}$指定的量子位時,結果 $0$ 會以機率 $|\alpha|^2$ 取得,而結果 $1$ 則為 probability $|\beta|^2。$ 在結果 $0 上,量子位的新狀態為 $ 1 0$\begin{bmatrix};在結果 \\1\end{bmatrix}$$ 上,其狀態為 $ 0 $\begin{bmatrix} 1 \\。\end{bmatrix}$ 請注意,這些機率加總起來是$1$,因為正規化條件是$|\alpha|^2 + |\beta|^2 = 1$。
測量的屬性也表示量子狀態向量的整體符號是無關緊要的。 否定向量相當於 $\alpha\right箭號 -\alpha$ 和 $\beta\right箭號 -\beta$ 。 由於測量 $0$ 和 $1$ 的機率取決於詞彙的大小平方,因此插入這類符號並不會改變機率。 這類階段通常稱為 "global phases"而且更通常可以是 e^$i { 格式\phi}$,而不只是 $\pm 1$。
測量的最終重要屬性是,它不一定會損害所有量子狀態向量。 從狀態 $\begin{bmatrix} 1 \\ 0 \end{bmatrix}$開始的量子位元,這對應於傳統狀態 $0$,測量此狀態時總會產生結果 $0$,且量子狀態保持不變。 從這個意義上說,如果只有傳統位(例如,$\begin{bmatrix}1 \\ 0 \end{bmatrix}$ 的量子位,或 $\begin{bmatrix}0 \\ 1 \end{bmatrix}$),則測量不會損壞系統。 這表示一個人可以在量子計算機上復寫傳統數據,並在量子計算機上操作它,就像在傳統計算機上一樣。 不過,一次將資訊儲存在兩種狀態的能力,正是量子運算超越傳統計算能力的關鍵,並進一步限制量子計算機任意複製量子數據的能力,另 請參閱無複制定理。
使用 Bloch 球體可視化量子位和轉換
量子位元也可以使用布洛赫球體表示法來描繪於$3$D。 Bloch 球可讓您將單一量子位量子狀態(這是二維複雜向量)描述為三維實值向量。 這很重要,因為它可讓我們可視化單一量子位狀態,進而開發理解多量子位狀態的寶貴推理(可悲的是 Bloch 球體表示法中斷)。 Bloch 球體可以可視化,如下所示:
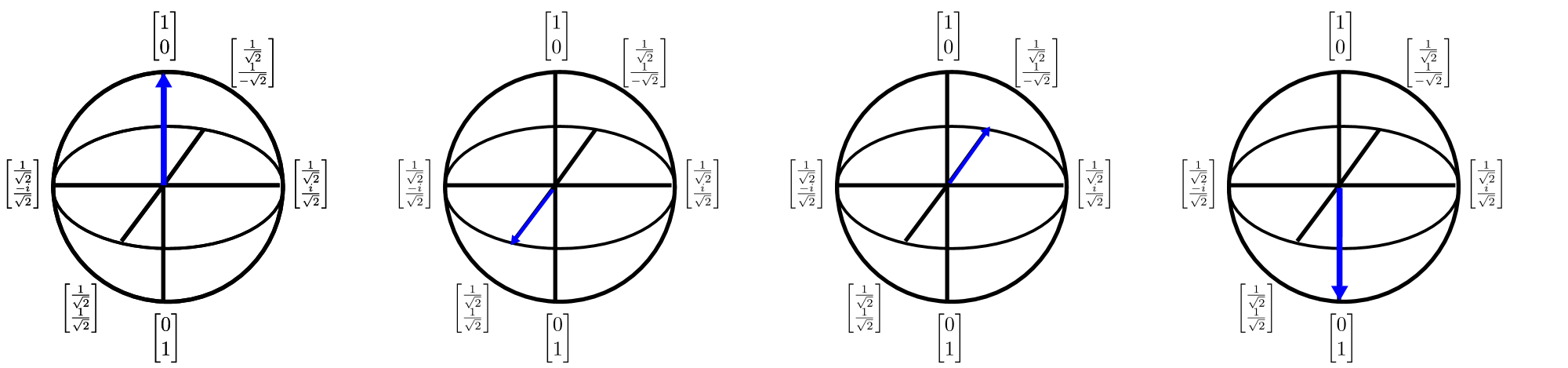
此圖表中的箭號會顯示量子狀態向量指向的方向,而箭號的每個轉換都可以視為一個基數座標軸的旋轉。 雖然將量子計算視為一連串旋轉是一種強大的直覺,但使用此直覺來設計和描述演算法是一項挑戰。 Q# 藉由提供描述這類輪替的語言來減輕此問題。
單量子位操作
量子電腦會使用一組通用的量子閘來處理數據,可以模擬量子狀態向量的任意旋轉。 這種通用概念類似於傳統(例如傳統)運算的普遍性概念,如果輸入位的每個轉換都可以使用有限長度電路來執行,網關集就會被視為通用。 在量子運算中,我們允許在量子位上執行的有效轉換是單一轉換和測量。 相鄰 運算 或複雜串連轉置對於量子運算至關重要,因為它需要反轉量子轉換。
單一量子位作業或單一量子位量子網關可分為兩個類別:Clifford 閘道和非 Clifford 閘道。 非克利福德門只包含 $T$ 門(也稱為 $\pi/8$ 門)。
$$ T=\begin{bmatrix} 1 & 0 \ 0 & e^{i\pi/4}\end{bmatrix}。 $$
默認包含在Q#中的單比特Clifford閘道的標準集合包括
$$ H=\frac{{1}{\sqrt{{2}}\begin{bmatrix} 1 &1 \ 1 &-1 \end{bmatrix} ,\qquad S =\begin{bmatrix} 1 &0 \ 0 &i \end{bmatrix}= T^2, \qquad X=\begin{bmatrix} 0 &1 \ 1&0 \end{bmatrix}= HT^4H, $$
$$ Y =\begin{bmatrix} 0 &-i \ i &0 \end{bmatrix}=T^2HT^4 HT^6, \qquad Z=\begin{bmatrix}1&0\ 0&-1 \end{bmatrix}=T^4。 $$
在這裡,作業 $X$、 $Y$ 和 $Z$ 特別頻繁使用,並以其創作者沃爾夫岡·保利的名字命名 為 Pauli 運算符 。 這些操作可以與非 Clifford 閘($T 閘$)一起組成,以近似單個量子位上的任何酉轉換。
儘管之前提到的那些是用來描述堆疊邏輯層的最常見原始閘門(將邏輯層視為量子演算法的層級),但在演算法層考慮一些較不基本的操作通常更為便利,例如那些更接近於函式描述層級的操作。 幸運的是,Q# 也有方法可以用來實作較高層級的單位運算,從而允許在不必明確地將所有專案分解到 Clifford 和 $T-門$的情況下實作高階演算法。
最簡單的這類基本類型是單一量子位旋轉。 一般會考慮三個單一量子位旋轉: $R_x$、 $R_y$ 和 $R_z$。 例如,若要可視化旋轉$R_x(\theta)$的動作,想像一下,將右拇指指向 Bloch 球體 X$ 軸的方向$,並透過 \theta/2$ 弧度的角度$旋轉向量。 這種令人困惑的 $2$ 因素源於在 Bloch 球體上繪製時,正交向量 $相隔 180^\circ$ ,但實際上 $以幾何方式相隔 90^\circ$ 度。 對應的單一矩陣如下:
$$ \begin{對齊*}&R_z(\theta) = e^{-i\theta Z/2}=\begin{bmatrix} e^{-i\theta/2}&0\\ 0&e^{i\theta/2}\end{bmatrix}, \\&R_x(\theta) = e^{-i\theta X/2}= HR_z(\theta)H =\begin{bmatrix} \cos(\theta/2) &-i\sin(\theta/2)\\ -i\sin(\theta/2) &\cos(\theta/2) \end{bmatrix},\\&R_y(\theta) = e^{-i\theta Y/2}= SHR_z(\theta)HS^\dagger=\begin{bmatrix} \cos(\theta/2) &-\sin(\theta/2)\\ \sin(\theta/2) &\cos(\theta/2) \end{bmatrix}。 \end{對齊*}$$
就像任何三個旋轉都可以結合在一起,以在三個維度中執行任意旋轉一樣,從 Bloch 球體表示中可以看到任何一元矩陣也可以撰寫為三個旋轉序列。 具體來說,對於每個酉矩陣$U$,存在$\alpha、\beta、\gamma、\delta$,使得$U= = e^{i\alpha} R_x(\beta)R_z(\gamma)R_x(\delta)$。 因此,$R_z(\theta)$ 和 $H$ 也會形成通用網關集,雖然它不是離散集合,因為 $\theta$ 可以接受任何值。 因此,由於量子模擬中的應用程式,這類連續網關對於量子計算至關重要,特別是在量子演算法設計層級。 為了達成具容錯功能的硬體實現,它們最終會編譯成接近這些旋轉的離散閘門序列。