Teori algoritma pencarian Grover
Pada artikel ini Anda akan menemukan penjelasan teoritis terperinci tentang prinsip-prinsip matematika yang membuat algoritma Grover bekerja.
Untuk implementasi praktis algoritma Grover untuk memecahkan masalah matematika, lihat Menerapkan algoritma pencarian Grover.
Pernyataan masalah
Algoritma Grover mempercepat solusi untuk pencarian data yang tidak terstruktur (atau masalah pencarian), menjalankan pencarian dalam langkah yang lebih sedikit daripada algoritma klasik apa pun. Setiap tugas pencarian dapat dinyatakan dengan fungsi abstrak $f(x)$ yang menerima item pencarian $x$. Jika item $x$ adalah solusi untuk tugas pencarian, maka $f(x)=1$. Jika item $x$ bukan solusi, maka $f(x)=0$. Masalah pencarian terdiri dari menemukan item $x_0$ apa pun sedemikian rupa sehingga $f(x_0)=1$.
Memang, masalah apa pun yang memungkinkan Anda untuk memeriksa apakah nilai $x$ tertentu adalah solusi yang valid (kuotasi &; ya atau tidak ada masalah&kuota;) dapat dirumuskan dalam hal masalah pencarian. Berikut ini adalah beberapa contoh:
- Masalah kepuasan Boolean: Apakah kumpulan nilai $Boolean x$ interpretasi (penugasan nilai ke variabel) yang memenuhi rumus Boolean yang diberikan?
- Masalah penjual keliling: Apakah $x$ menjelaskan perulangan sesingkat mungkin yang menghubungkan semua kota?
- Masalah pencarian database: Apakah tabel database berisi rekaman $x$?
- Masalah faktorisasi bilangan bulat: Apakah angka $tetap N$ dapat dibagi berdasarkan angka $x$?
Tugas yang algoritma Grover bertujuan untuk memecahkan dapat dinyatakan sebagai berikut: mengingat fungsi klasik $f(x):\{0,1\}^n \rightarrow\{0,1\}$, di mana $n$ merupakan bit-size dari ruang pencarian, temukan input $x_0$ yang $f(x_0)=1$. Kompleksitas algoritma diukur dengan jumlah penggunaan fungsi $f(x)$. Secara klasik, dalam skenario terburuk, $f(x)$ harus dievaluasi total $N-1$ kali, di mana $N=2^n$, mencoba semua kemungkinan. Setelah elemen $N-1$, elemen tersebut harus menjadi elemen terakhir. Algoritma kuantum Grover dapat memecahkan masalah ini lebih cepat, memberikan kecepatan kuadrat. Kuadrat di sini menyiratkan bahwa hanya tentang evaluasi $\sqrt{N}$ yang diperlukan, dibandingkan dengan $N$.
Garis besar algoritma
Misalkan ada item $N=2^n$ yang memenuhi syarat untuk tugas pencarian dan mereka adalah indeks dengan menetapkan setiap item bilangan bulat dari $0$ sampai $N-1$. Selanjutnya, misalkan ada $M$ input valid yang berbeda, yang berarti bahwa ada input $M$ yang $f(x)=1$. Langkah-langkah algoritma adalah sebagai berikut:
- Mulailah dengan daftar $n$ qubit yang diinsialisasi di status $\ket{0}$.
- Siapkan register ke dalam superposisi seragam dengan menerapkan $H$ ke setiap qubit register: $$|\text{register}\rangle=\frac{1}{\sqrt{N}}\sum_{x=0}^{N-1}|x\rangle$$
- Terapkan operasi berikut ke waktu register $N_{\text{optimal}}$ :
- Oracle fase $O_f$ yang menerapkan pergeseran fase bersyarat $-1$ untuk item solusi.
- Terapkan $H$ ke setiap qubit dalam register.
- Pergeseran fase bersyarat $-1$ ke setiap kondisi dasar komputasi kecuali $\ket{0}$. Ini dapat diwakili oleh operasi $kesatuan -O_0$, karena $O_0$ mewakili pergeseran fase bersyarat menjadi hanya $\ket{0}$.
- Terapkan $H$ ke setiap qubit dalam register.
- Ukur register untuk mendapatkan indeks item yang merupakan solusi dengan probabilitas yang sangat tinggi.
- Periksa apakah itu solusi yang valid. Jika tidak, mulailah lagi.
$N_\text{optimal}=\left\lfloor \frac{\pi}{{4}\sqrt{\frac{N}{M}}-\frac{1}{{2}\right\rfloor$ adalah jumlah iterasi optimal yang memaksimalkan kemungkinan mendapatkan item yang benar dengan mengukur register.
Catatan
Aplikasi bersama dari langkah-langkah 3.b, 3.c dan 3.d biasanya dikenal dalam literatur sebagai operator difusi Grover.
Operasi kesatuan keseluruhan yang diterapkan pada register adalah:
$$(-H^{\otimes n}O_0H^{\otimes n}O_f)^{N_{\text{optimal}}}H^{\otimes n}$$
Mengikuti status register langkah demi langkah
Untuk mengilustrasikan prosesnya, mari kita ikuti transformasi matematis dari kondisi register untuk kasus sederhana di mana hanya ada dua qubit dan elemen yang valid adalah $\ket{01}.$
Register dimulai status: $$|\text{register}\rangle=|00\rangle$$
Setelah menerapkan $H$ ke setiap qubit, status register berubah menjadi: $$|\text{register}\rangle=\frac{{1}{\sqrt{{4}}\sum_{i \in \{0,1\}^2}|i\rangle=\frac12(\ket{00}+\ket{01}+\ket{10}+\ket{11})$$
Kemudian, oracle fase diterapkan untuk mendapatkan: $$|\text{register}\rangle=\frac12(\ket{{00}-\ket{{01}+\ket{{10}+\ket{{11})$$
Kemudian $H$ bertindak pada setiap qubit lagi untuk memberikan: $$|\text{register}\rangle=\frac12(\ket{{00}+\ket{{01}-\ket{{10}+\ket{{11})$$
Sekarang pergeseran fase bersyarat diterapkan pada setiap kondisi kecuali $\ket{00}$: $$|\text{register}\rangle=\frac12(\ket{{00}-\ket{{01}+\ket{{10}-\ket{{11})$$
Akhirnya, iterasi Grover pertama berakhir dengan menerapkan $H$ lagi untuk mendapatkan: $$|\text{register}\rangle=\ket{{01}$$
Dengan mengikuti langkah-langkah di atas, item yang valid ditemukan dalam satu iterasi. Seperti yang akan Anda lihat nanti, ini karena untuk N=4 dan satu item yang valid, $N_\text{optimal}=1$.
Penjelasan geometris
Untuk melihat mengapa algoritma Grover bekerja, mari kita pelajari algoritma dari perspektif geometris. Biarkan $\ket{\text{buruk}}$ menjadi superposisi dari semua status yang bukan solusi untuk masalah pencarian. Misalkan ada solusi $M$ yang valid:
$$\ket{\text{bad}}=\frac{{1}{\sqrt{N-M}}\sum_{x:f(x)=0}\ket{x}$$
$\ket{\text{Kebaikan}}$ status didefinisikan sebagai superposisi semua status yang merupakan solusi untuk masalah pencarian:
$$\ket{\text{good}}=\frac{{1}{\sqrt{M}}\sum_{x:f(x)=1}\ket{x}$$
Dikarenakan baik dan buruk adalah set yang saling eksklusif karena suatu item tidak dapat valid dan tidak valid, status $\ket{\text{baik}}$ dan $\ket{\text{buruk}}$ adalah ortogonal. Kedua status membentuk dasar ortogonal dari bidang di ruang vektor. Seseorang dapat menggunakan bidang ini untuk memvisualisasikan algoritma.
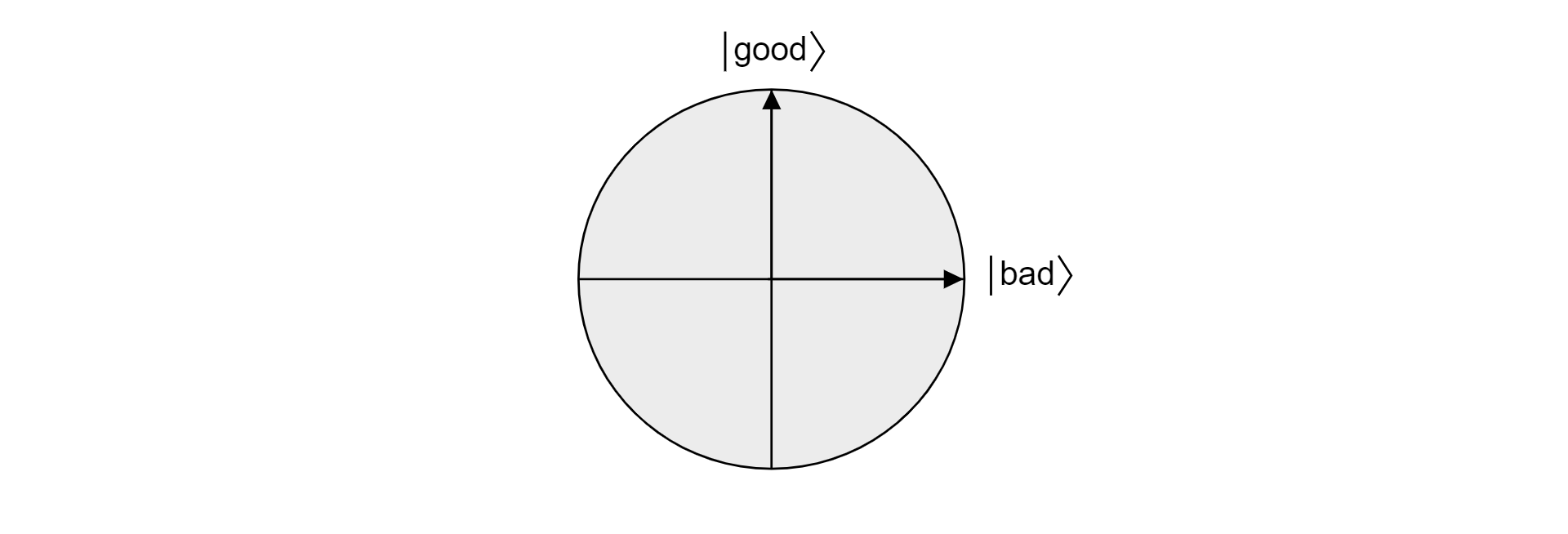
Sekarang, misalkan $\ket{\psi}$ adalah kondisi arbitrary yang hidup di pesawat yang membentang oleh $\ket{\text{baik}}$ dan $\ket{\text{buruk}}$. Setiap status yang tinggal di pesawat itu dapat dinyatakan sebagai:
$$\ket{\psi}=\alpha\ket{\text{baik}} + \beta\ket{\text{buruk}}$$
di mana $\alpha$ dan $\beta$ adalah bilangan real. Sekarang, mari kita perkenalkan operator refleksi $R_{\ket{\psi}}$, di mana $\ket{\psi}$ kondisi qubit yang tinggal di pesawat. Operator didefinisikan sebagai:
$$R_{\ket{\psi}}=2\ket{\psi}\bra{\psi}-\mathcal{I}$$
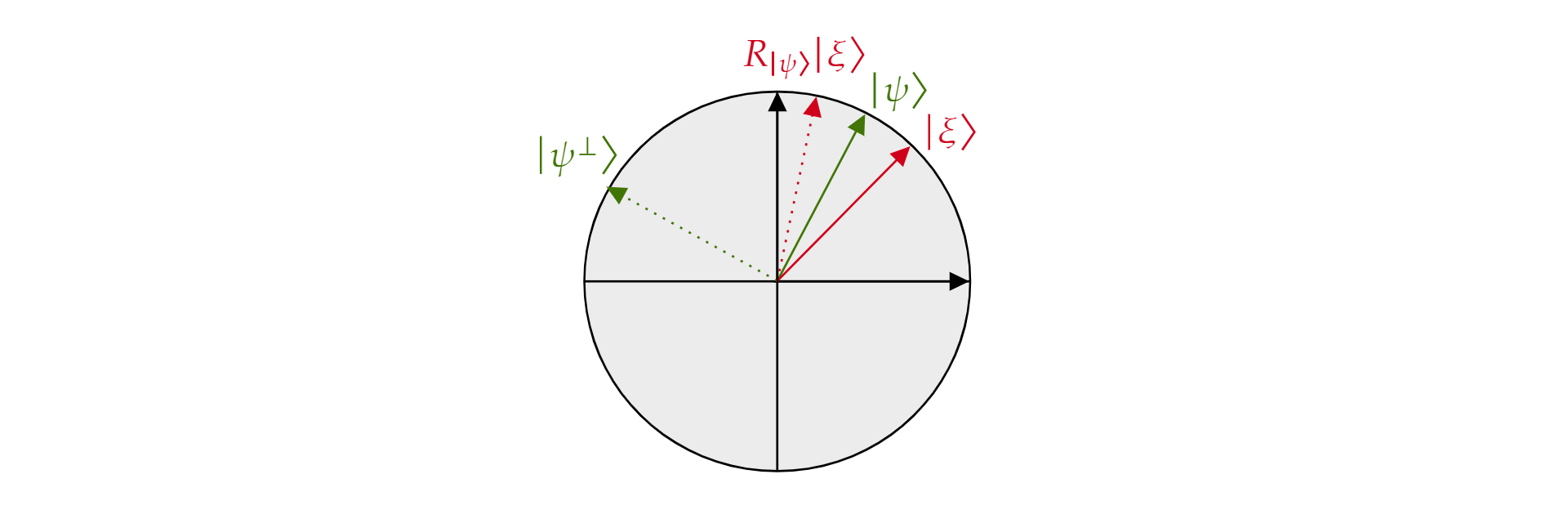
Ini disebut operator refleksi tentang $\ket{\psi}$ karena dapat ditafsirkan secara geometris sebagai refleksi tentang arah $\ket{\psi}$. Untuk melihatnya, ambil dasar ortogonal dari bidang yang dibentuk oleh $\ket{\psi}$ dan pelengkap $\ket{\psi^{\perp}}$ ortogonalnya. Setiap kondisi $\ket{\xi}$ pesawat dapat diuraikan dalam dasar seperti:
$$\ket{\xi}=\mu \ket{\psi} + \nu {\ket{\psi^{\perp}}}$$
Jika salah satu menerapkan operator $R_{\ket{\psi}}$ to $\ket{\xi}$:
$$R_{\ket{\psi}}\ket{\xi}=\mu \ket{\psi} - \nu {\ket{\psi^{\perp}}}$$
Operator $R_\ket{\psi}$ membalikkan komponen orthogonal ke $\ket{\psi}$ tetapi membiarkan komponen $\ket{\psi}$ tidak berubah. Oleh karena itu, $R_\ket{\psi}$ adalah refleksi tentang $\ket{\psi}$.
Algoritma Grover, setelah aplikasi pertama $H$ untuk setiap qubit, dimulai dengan superposisi seragam dari semua status. Ini dapat ditulis sebagai:
$$\ket{\text{all}}=\sqrt{\frac{M}{N}}\ket{\text{good}} + \sqrt{\frac{N-M}{N}}\ket{\text{bad}}$$
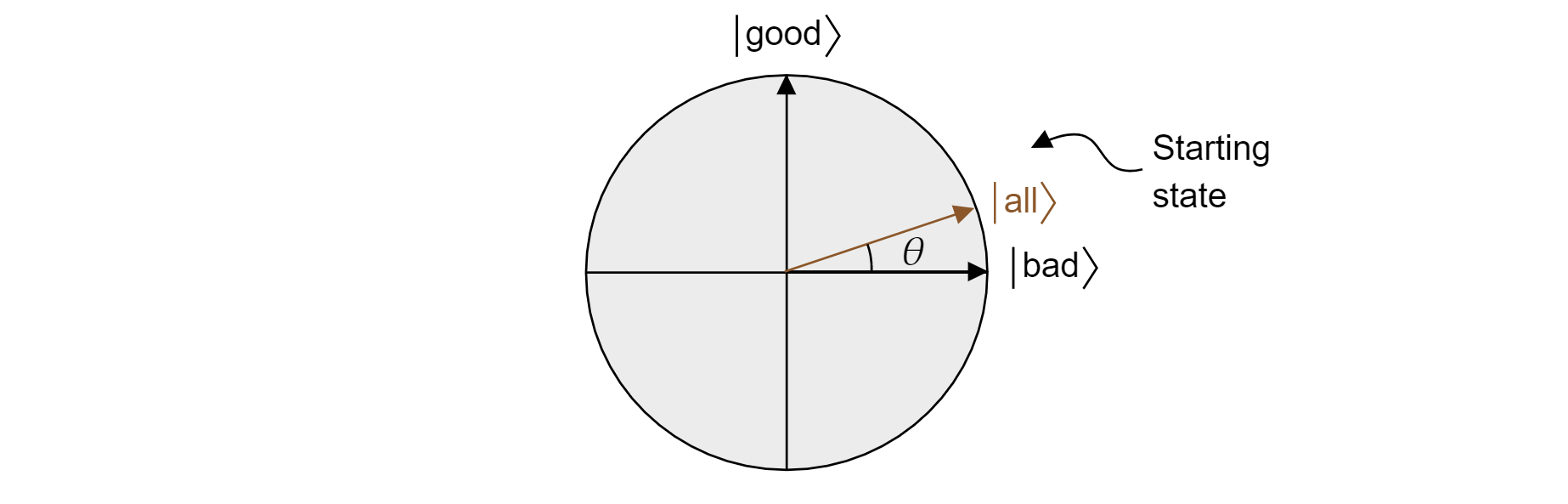
Dan dengan demikian status tinggal di pesawat. Perhatikan bahwa probabilitas mendapatkan hasil yang benar ketika mengukur dari superposisi yang sama hanya $|\braket{\text{baik}|{\text{semua}}}|^2=M/N$, yang akan Anda harapkan dari tebakan acak.
Oracle $O_f$ menambahkan fase negatif ke solusi apa pun untuk masalah pencarian. Oleh karena itu, dapat ditulis sebagai refleksi tentang sumbu $\ket{\text{buruk}}$ :
$$O_f = R_{\ket{\text{bad}}}= 2\ket{\text{bad}}\bra{\text{bad}} - \mathcal{I}$$
Analoginya, pergeseran fase bersyarat $O_0$ hanyalah refleksi terbalik tentang kondisi $\ket{0}$:
$$O_0 = R_{\ket{0}}= -2\ket{{0}\bra{0} + \mathcal{I}$$
Mengetahui fakta ini, mudah untuk memeriksa bahwa operasi difusi Grover -H $-H^{\otimes n} O_0 H^{\otimes n}$ juga merupakan refleksi tentang kondisi $\ket{semua}$. Lakukan saja:
$$-H^{\otimes n} O_0 H^{\otimes n}=2H^{\otimes n}\ket{0}\bra{{0}H^{\otimes n} -H^{\otimes n}\mathcal{I}H^{\otimes n}= 2\ket{\text{all}}\bra{\text{all}} - \mathcal{I}= R_{\ket{\text{all}}}$$
Telah ditunjukkan bahwa setiap iterasi algoritma Grover adalah komposisi dari dua refleksi $R_\ket{\text{bad}}$ dan $R_\ket{\text{semua}}$.
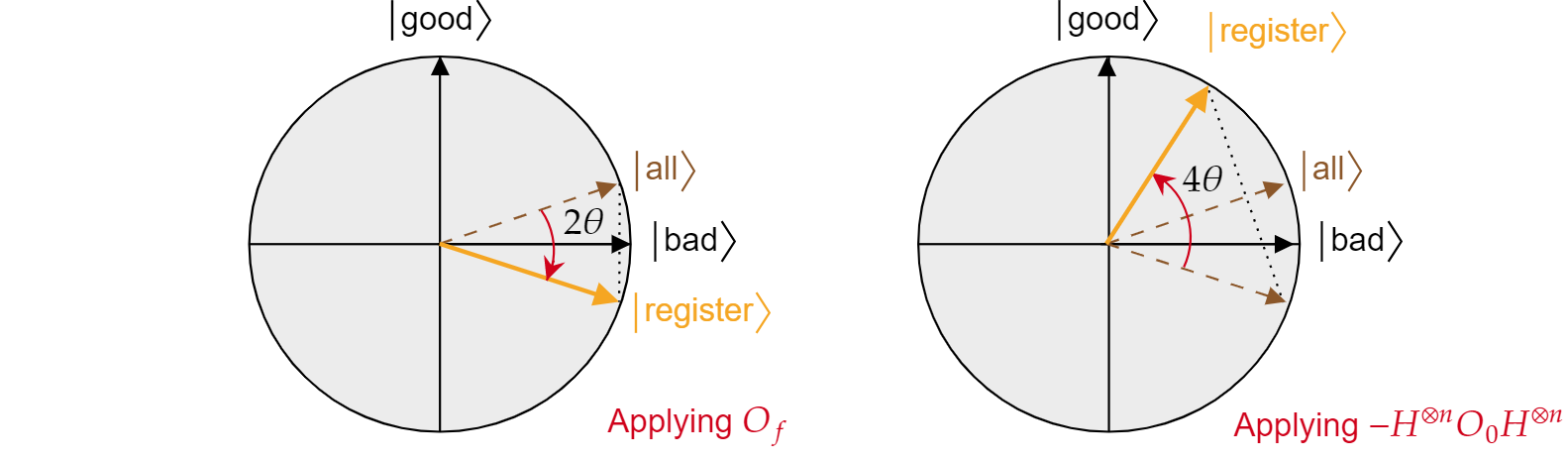
Efek gabungan dari setiap iterasi Grover adalah rotasi berlawanan arah jarum jam dari sudut $2\theta$. Untungnya, sudut $\theta$ mudah ditemukan. Karena $\theta$ hanyalah sudut antara $\ket{\text{semua}}$ dan $\ket{\text{buruk}}$, seseorang dapat menggunakan produk skalar untuk menemukan sudutnya. Diketahui bahwa $\cos{\theta}=\braket{\text{all}|\text{bad}}$, jadi seseorang perlu menghitung $\braket{\text{all}|\text{bad}}$. Dari dekomposisi $\ket{\text{semua}}$ dalam hal $\ket{\text{buruk}}$ dan $\ket{\text{baik}}$, berikut:
$$\theta = \arccos{\left(\braket{\text{all}|\text{bad}}\right)}= \arccos{\left(\sqrt{\frac{N-M}{N}}\right)}$$
Sudut antara status register dan $\ket{\text{status yang baik}}$ berkurang dengan setiap iterasi, menghasilkan probabilitas yang lebih tinggi untuk mengukur hasil yang valid. Untuk menghitung probabilitas ini, Anda hanya perlu menghitung $|\braket{\text{register}}|^2$ yang baik}|\text{. Menunjukkan sudut antara $\ket{\text{baik}}$ dan $\ket{\text{register}}$$\gamma (k)$, di mana $k$ adalah jumlah iterasi:
$$\gamma (k) =\frac{\pi}{2}-\theta -k2\theta =\frac{\pi}{{2} -(2k + 1) \theta $$
Oleh karena itu, probabilitas keberhasilan adalah:
$$P(\text{success}) = \cos^2(\gamma(k)) = \sin^2\left[(2k +1)\arccos \left( \sqrt{\frac{N-M}{N}}\right)\right]$$
Jumlah iterasi yang optimal
Karena probabilitas keberhasilan dapat ditulis sebagai fungsi dari jumlah iterasi, jumlah optimal iterasi $N_{\text{optimal}}$ dapat ditemukan dengan menghitung bilangan bulat positif terkecil yang (kira-kira) memaksimalkan fungsi probabilitas keberhasilan.
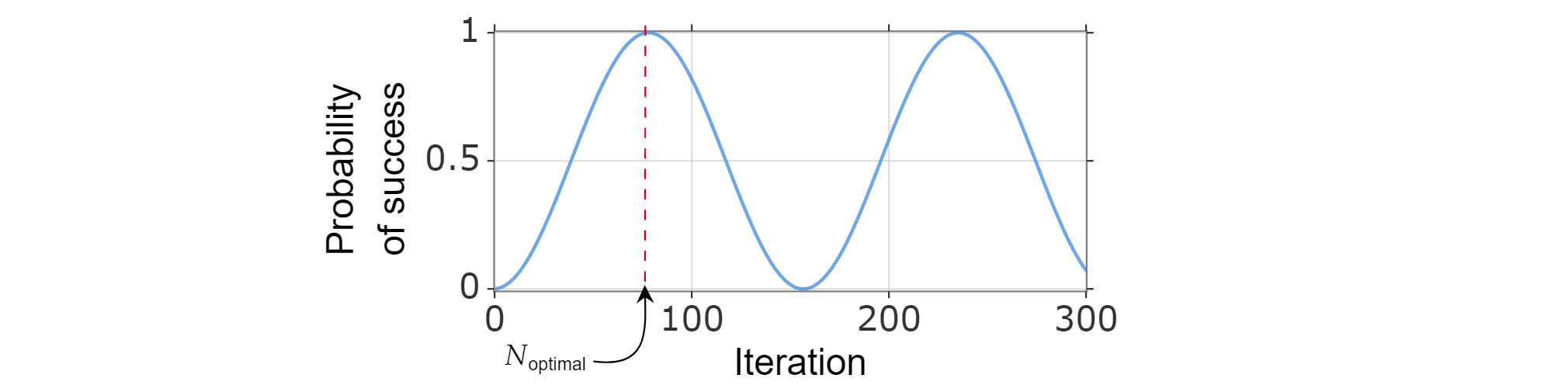
Diketahui bahwa $\sin^2{x}$ mencapai maksimum pertama untuk $x=\frac{\pi}{2}$, jadi:
$$\frac{\pi}{{2}=(2k_{\text{optimal}} +1)\arccos \left( \sqrt{\frac{N-M}{N}}\right)$$
Ini memberikan:
$$k_{\text{optimal}}=\frac{\pi}{4\arccos\left(\sqrt{1-M/N}\right)}-1/2 =\frac{\pi}{{4}\sqrt{\frac{N}{M}}-\frac{1}{2}-O\left(\sqrt\frac{M}{N}\right)$$
Di mana pada langkah terakhir, $\arccos \sqrt{1-x}=\sqrt{x} + O(x^{3/2})$.
Oleh karena itu, Anda dapat memilih $N_\text{optimal}$ menjadi $N_\text{optimal\left}=\lfloor \frac{\pi}{{4}\sqrt{\frac{N}{M}}-\frac{{1}{2}\right\rfloor$.
Analisis kompleksitas
Dari analisis sebelumnya, kueri $O\left(\sqrt{\frac{N}{M}}\right)$ dari oracle $O_f$ diperlukan untuk menemukan item yang valid. Namun, dapatkah algoritma diimplementasikan secara efisien dalam hal kompleksitas waktu? $O_0$ didasarkan pada komputasi operasi Boolean pada $n$ bit dan diketahui dapat diimplementasikan menggunakan gerbang $O(n)$. Ada juga dua lapisan $n$ gerbang Hadamard. Kedua komponen ini dengan demikian hanya membutuhkan gerbang $O(n)$ per iterasi. Karena $N=2^n$, maka $O(n)=O(log(N))$. Oleh karena itu, jika iterasi $O\left(\sqrt{\frac{N}{M}}\right)$ dan gerbang $O(log(N))$ per iterasi diperlukan, kompleksitas total waktu (tanpa memperhitungkan implementasi oracle) adalah $O\left(\sqrt{\frac{N}{M}}log(N)\right)$.
Kompleksitas keseluruhan algoritma pada akhirnya tergantung pada kompleksitas implementasi O_f$ oracle$. Jika evaluasi fungsi jauh lebih rumit pada komputer kuantum daripada pada yang klasik, runtime algoritma keseluruhan akan lebih lama dalam kasus kuantum, meskipun secara teknis, ia menggunakan lebih sedikit kueri.
Referensi
Jika Anda ingin terus belajar tentang algoritma Grover, Anda dapat memeriksa salah satu sumber berikut:
- Karya ilmiah asli oleh Lov K. Grover
- Algoritma pencarian kuantum bagian Nielsen, M. A. &Amp; Chuang, I. L. (2010). Quantum Computation and Quantum Information.
- Algoritma Grover tentang Arxiv.org