Qubit dalam komputasi kuantum

  • Artikel

Sama seperti bit yang merupakan objek dasar informasi dalam komputasi klasik, qubit (bit kuantum) adalah objek fundamental informasi dalam komputasi kuantum. Untuk memahami korespondensi ini, artikel ini menjelaskan contoh paling sederhana: qubit tunggal.

Mewakili qubit

Bit, atau digit biner, dapat memiliki nilai $0$ atau $1$, qubit dapat memiliki nilai $0$, $1$ atau superposisi kuantum $0$ dan $1$.

Keadaan qubit tunggal dapat dijelaskan oleh vektor kolom dua dimensi dari norma unit, yaitu, besarnya kuadrat dari entri harus berjumlah $1$. Vektor ini, yang disebut vektor keadaan kuantum, menyimpan semua informasi yang diperlukan untuk menggambarkan sistem kuantum satu qubit sama seperti satu bit memegang semua informasi yang diperlukan untuk menggambarkan keadaan variabel biner. Untuk dasar-dasar vektor dan matriks dalam komputasi kuantum, lihat Aljabar linier untuk komputasi kuantum dan Vektor dan matriks.

Setiap vektor kolom dua dimensi dari bilangan real atau kompleks dengan norma $1$ mewakili keadaan kuantum yang mungkin dipegang oleh qubit. Dengan demikian $\begin{bmatrix}\alpha\\\beta\end{bmatrix}$mewakili keadaan qubit jika $\alpha$ dan $\beta$ merupakan bilangan kompleks yang memenuhi $|\alpha|^2 + |\beta|^2 = 1$. Beberapa contoh vektor keadaan kuantum yang valid yang mewakili qubit termasuk

$$\begin{bmatrix} 1 \\ 0 \end{bmatrix}, \begin{bmatrix} 0 \\ 1 \end{bmatrix}, \begin{bmatrix}\frac{{1}{\sqrt{2}}\\\frac{{1}{\sqrt{2}}\end{bmatrix}, \begin{bmatrix}\frac{1}{\sqrt{{2}}\\\frac{{-1}{\sqrt{2}}\end{bmatrix}, \text{ dan }\begin{bmatrix}\frac{1}{\sqrt{{2}}\\\frac{i}{\sqrt{2}}\end{bmatrix}.$$

Vektor keadaan kuantum $\begin{bmatrix} 1 \\ 0 \end{bmatrix}$ dan $\begin{bmatrix} 0 \\ 1 \end{bmatrix}$ mendapatkan peran khusus. Kedua vektor ini membentuk dasar untuk ruang vektor yang menggambarkan keadaan qubit. Ini berarti bahwa setiap vektor keadaan kuantum dapat ditulis sebagai jumlah vektor dasar ini. Secara khusus, vektor $\begin{bmatrix} x \\ y \end{bmatrix}$ dapat ditulis sebagai $x \begin{bmatrix} 1 \\ 0 \end{bmatrix} + y \begin{bmatrix} 0 \\ 1 \end{bmatrix}$. Sementara setiap rotasi vektor ini akan berfungsi sebagai dasar yang sangat valid untuk qubit, yang satu ini dipilih, dengan menyebutnya dasar komputasi.

Kedua keadaan kuantum ini diambil agar sesuai dengan dua keadaan bit klasik, yaitu $0$ dan $1$. Konvensi standar adalah memilih

$$0\equiv\begin{bmatrix} 1 \\ 0 \end{bmatrix}, \qquad 1 \equiv\begin{bmatrix} 0 \\ 1 \end{bmatrix},$$

meskipun pilihan yang berlawanan juga bisa diambil dengan baik. Dengan demikian, dari jumlah tak terbatas kemungkinan vektor keadaan kuantum qubit tunggal, hanya dua yang sesuai dengan keadaan bit klasik; semua keadaan kuantum lainnya tidak.

Mengukur qubit

Cara mewakili qubit yang dijelaskan, seseorang dapat memperoleh intuisi untuk apa yang diwakili oleh keadaan ini dengan membahas konsep pengukuran. Pengukuran sesuai dengan gagasan informal dari "melihat" qubit, yang segera meruntuhkan keadaan kuantum ke salah satu dari dua keadaan klasik $\begin{bmatrix} 1 \\ 0 \end{bmatrix}$ atau $\begin{bmatrix} 0 \\ 1 \end{bmatrix}$. Saat qubit yang diberikan oleh vektor keadaan kuantum $\begin{bmatrix}\alpha\\\beta\end{bmatrix}$ diukur, hasil $0$ diperoleh dengan probabilitas $|\alpha|^ 2$ dan hasil $1$ dengan probabilitas $|\beta|^ 2.$ Pada hasil $0$, keadaan baru qubit adalah $\begin{bmatrix} 1 \\ 0 \end{bmatrix}$; pada hasil $1$ keadaannya adalah $\begin{bmatrix} 0 \\ 1 \end{bmatrix}$. Perhatikan bahwa probabilitas ini berjumlah hingga $1$ karena kondisi normalisasi $|\alpha|^2 + |\beta|^2 = 1$.

Sifat pengukuran juga berarti bahwa tanda keseluruhan vektor keadaan kuantum tidak relevan. Meniadakan vektor setara dengan panah $\alpha\right -\alpha$ dan panah $\beta\right -\beta$. Karena probabilitas mengukur $0$ dan $1$ bergantung pada besarnya kuadrat dari ketentuan, memasukkan tanda-tanda tersebut tidak mengubah probabilitas sama sekali. Fase seperti itu biasa disebut "fase global" dan lebih umum dapat berupa bentuk $e^{i \phi}$ bukan hanya $\pm 1$.

Properti penting terakhir dari pengukuran adalah bahwa hal itu tidak selalu merusak semua vektor keadaan kuantum. Jika seseorang mulai dengan qubit di keadaan $\begin{bmatrix} 1 \\ 0 \end{bmatrix}$, yang sesuai dengan keadaan $klasik 0$, mengukur keadaan ini akan selalu menghasilkan hasil $0$ dan membiarkan keadaan kuantum tidak berubah. Dalam pengertian ini, jika hanya ada bit klasik (misalnya, qubit yang merupakan $\begin{bmatrix}1 \\ 0 \end{bmatrix}$ atau $\begin{bmatrix}0 \\ 1 \end{bmatrix}$) maka pengukuran tidak merusak sistem. Ini berarti bahwa seseorang dapat mereplikasi data klasik dan memanipulasinya pada komputer kuantum seperti yang dapat dilakukan pada komputer klasik. Namun, kemampuan untuk menyimpan informasi di kedua keadaan sekaligus adalah kemampuan yang meningkatkan komputasi kuantum di luar apa yang biasanya dimungkinkan dan kemudian merampas kemampuan komputer kuantum untuk menyalin data kuantum tanpa pandang bulu, lihat juga teorema tanpa kloning.

Memvisualisasikan qubit dan transformasi menggunakan lingkup bloch

Qubit juga dapat digambarkan dalam $3$D menggunakan representasi lingkup Bloch. Lingkup Bloch memberikan cara untuk menggambarkan keadaan kuantum qubit tunggal (yang merupakan vektor kompleks dua dimensi) sebagai vektor bernilai nyata tiga dimensi. Hal ini penting karena memungkinkan kita memvisualisasikan keadaan qubit tunggal dan dengan demikian mengembangkan penalaran yang dapat sangat berharga dalam memahami keadaan multi-qubit (sayangnya, representasi lingkup Bloch rusak). Lingkup Bloch ini dapat divisualisasikan sebagai berikut:

Lingkup bloch

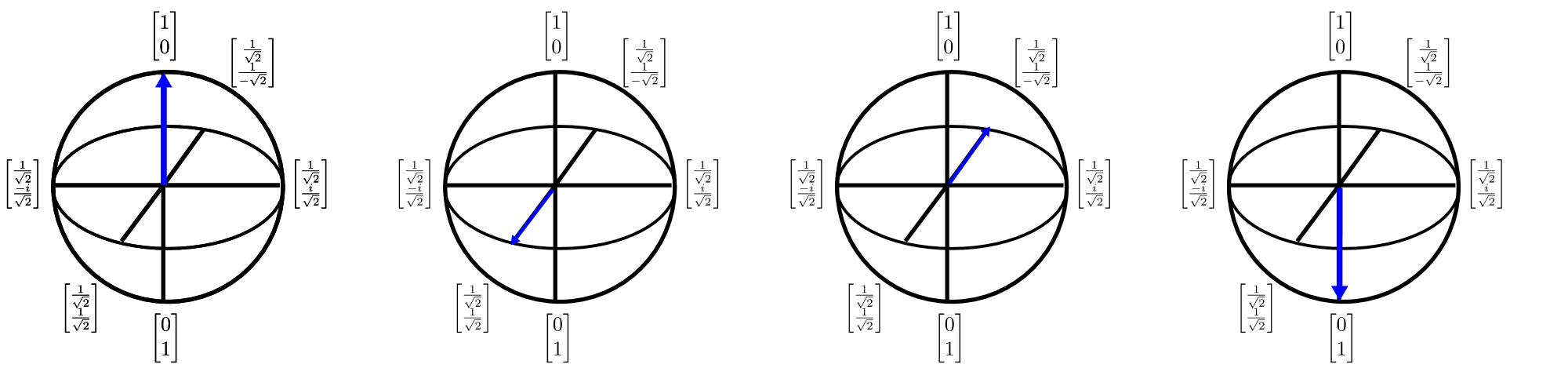
Panah dalam diagram ini menunjukkan arah vektor keadaan kuantum menunjuk dan setiap transformasi panah dapat dianggap sebagai rotasi tentang salah satu sumbu kardinal. Sementara menganggap perhitungan kuantum sebagai urutan rotasi adalah hal yang sulit dihilangkan, cukup menantang untuk menggunakan pemikiran ini guna merancang dan menggambarkan algoritma. Q# meringankan masalah ini dengan menyediakan bahasa untuk menggambarkan rotasi tersebut.

Operasi qubit tunggal

Komputer kuantum memproses data dengan menerapkan satu set universal gerbang kuantum yang dapat meniru rotasi vektor keadaan kuantum. Gagasan universalitas ini mirip dengan gagasan universalitas untuk komputasi tradisional (misalnya, klasik) saat set gerbang dianggap universal jika setiap transformasi bit input dapat dilakukan menggunakan sirkuit panjang terbatas. Dalam komputasi kuantum, transformasi valid yang diizinkan untuk kita lakukan pada qubit adalah transformasi dan pengukuran kesatuan. Operasi yang berdampingan atau transpos konjugat kompleks sangat penting untuk komputasi kuantum karena diperlukan untuk menginversi transformasi kuantum.

Operasi qubit tunggal, atau gerbang kuantum quantum tunggal dapat diklasifikasikan ke dalam dua kategori: gerbang Clifford dan gerbang non-Clifford. Gerbang Non-Clifford hanya terdiri dari $gerbang T$ (juga dikenal sebagai $gerbang \pi/8$ ).

$$T=\begin{bmatrix} 1 amp; 0 \\ 0 & e^{i\pi/4}\end{bmatrix}.& $$

Set standar gerbang Clifford qubit tunggal, dicakup secara default pada Q#, termasuk

$$ H=\frac{{1}{\sqrt{{2}}\begin{bmatrix} 1 & 1 \\ 1 &-1 \end{bmatrix} , \qquad S =\begin{bmatrix} 1 & 0 \\ 0 & i \end{bmatrix}= T^2, \qquad X=\begin{bmatrix} 0 & 1 \\ 1& 0 \end{bmatrix}= HT^4H, $$

$$ Y =\begin{bmatrix} 0 & -i i \\& 0 \end{bmatrix}=T^2HT^4 HT^6, \qquad Z=\begin{bmatrix}1& 0\\ 0&-1 \end{bmatrix}=T^4. $$

Di sini, operasi $X$, $Y$, dan $Z$ terutama sering digunakan dan diberi nama operator Pauli menurut penciptanya, Wolfgang Pauli. Bersama dengan gerbang non-Clifford (Gerbang-$T$), operasi ini dapat disusun untuk memperkirakan transformasi kesatuan pada satu qubit.

Sementara yang sebelumnya merupakan gerbang primitif yang paling populer untuk menggambarkan operasi pada tingkat logis tumpukan (pertimbangkan tingkat logis sebagai tingkat algoritma kuantum), seringkali lebih mudah untuk mempertimbangkan operasi yang kurang mendasar pada tingkat algoritmik, misalnya operasi lebih dekat ke tingkat deskripsi fungsi. Untungnya, Q# juga memiliki metode yang tersedia untuk menerapkan kesatuan tingkat yang lebih tinggi, yang pada gilirannya memungkinkan algoritma tingkat tinggi untuk diimplementasikan tanpa secara eksplisit menguraikan semuanya ke Clifford dan Gerbang-$T$.

Primitif yang paling sederhana adalah rotasi qubit tunggal. Tiga rotasi qubit tunggal biasanya dipertimbangkan: $R_x$, $R_y$, dan $R_z$. Untuk memvisualisasikan aksi rotasi $R_x(\theta)$, misalnya, bayangkan mengarahkan ibu jari kanan Anda di sepanjang arah sumbu $x$ lingkup Bloch dan memutar vektor dengan tangan Anda melalui sudut radian $\theta/2$. Faktor membingungkan dari $2$ ini muncul dari fakta bahwa vektor ortogonal $180^\circ$ saat diplot pada lingkup Bloch, namun sebenarnya $90^\circ$ terpisah secara geometris. Matriks kesatuan yang sesuai adalah:

\begin{ratakan*}& R_z(\theta) = e^{-i\theta Z/2}=\begin{bmatrix} e^{-i\theta/2}& 0\\ 0& e^{i\theta/2\end{bmatrix}}, \\& R_x(\theta) e^{-i\theta X/2=} HR_z(\theta)H =\begin{bmatrix} \cos(\theta/2) & -i\sin(\theta/2)\\ -i\sin(\theta/2) & \cos(\theta/2) \end{bmatrix}, \\& = R_y(\theta) e^-i\theta Y/2=} SHR_z(\theta)HS^\begin{bmatrix}=\dagger \cos(\theta/2) & -\sin(\theta/2)\\ \sin(\theta/2) & \cos(\theta/2) \end{bmatrix}.{= \end{align*}

Sama seperti tiga rotasi dapat digabungkan bersama untuk melakukan rotasi arbitrer dalam tiga dimensi, dapat dilihat dari representasi lingkup Bloch bahwa matriks kesatuan dapat ditulis sebagai urutan tiga rotasi juga. Secara khusus, untuk setiap matriks kesatuan $U$ terdapat $\alpha,\beta,\gamma,\delta$ sedemikian rupa sehingga $U= e^{i\alpha} R_x(\beta)R_z(\gamma)R_x(\delta)$. Dengan demikian $R_z (\theta)$ dan $H$ juga membentuk set gerbang universal meskipun bukan set diskrit karena $\theta$ dapat mengambil nilai apa pun. Untuk alasan ini, dan karena aplikasi dalam simulasi kuantum, gerbang kontinu seperti itu sangat penting untuk perhitungan kuantum, terutama pada tingkat desain algoritma kuantum. Untuk mencapai implementasi perangkat keras yang toleran terhadap kesalahan, pada akhirnya akan dikompilasi ke dalam urutan gerbang diskrit yang mendekati rotasi ini.

Langkah berikutnya