Konventioner för kvantkretsdiagram

Ibland är kvantalgoritmer lättare att förstå i ett kretsdiagram än i motsvarande skrivna matrisrepresentation. Den här artikeln beskriver hur du läser kvantkretsdiagram och deras konventioner.

Mer information finns i Så här visualiserar du diagram över kvantkretsar.

Läsa kvantkretsdiagram

I en kvantkrets flödar tiden från vänster till höger. Kvantgrindar sorteras i kronologisk ordning med den vänstra grinden eftersom grinden först appliceras på kvantbitarna.

Ta följande kvantkretsdiagram som exempel:

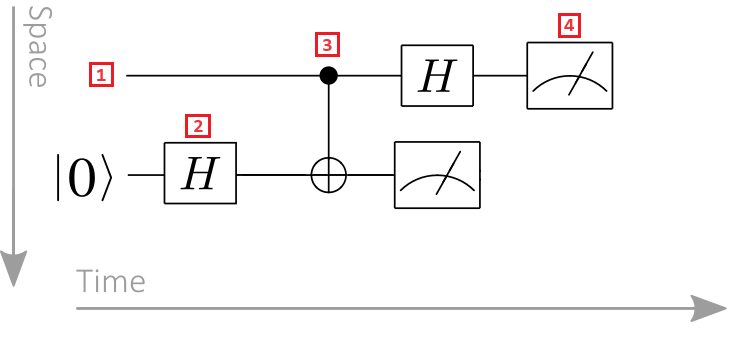
1. Qubitregister: Qubit-register visas som vågräta linjer, där varje rad representerar en qubit. Den översta raden är qubit-registret märkt 0, den andra raden är qubitregister märkt 1 och så vidare.
2. Kvantgrind: Kvantåtgärder representeras av kvantgrindar. Termen kvantgrind motsvarar klassiska logikgrindar. Grindar som agerar på en eller flera qubitregister betecknas som en ruta. I det här exemplet representerar symbolen en Hadamard-åtgärd.
3. Styrd grind: Kontrollerade grindar fungerar på två eller flera qubitar. I det här exemplet representerar symbolen en CNOT-grind. Den svarta cirkeln representerar kontrollkvabiten och korset i en cirkel representerar kvantbiten target .
4. Mätningsåtgärd: Mätarsymbolen representerar en mätningsåtgärd. Mätningsåtgärden tar ett qubitregister som indata och matar ut klassisk information.

Tillämpa kvantgrindar

Eftersom tiden flödar från vänster till höger tillämpas den vänstra grinden först Till exempel är åtgärden för följande kvantkrets den enhetliga matrisens $CBA$.

Kommentar

Matris multiplikation följer den motsatta konventionen: den högra matrisen tillämpas först. I kvantkretsdiagram tillämpas dock den vänstra grinden först. Den här skillnaden kan ibland leda till förvirring, så det är viktigt att notera den här betydande skillnaden mellan den linjära algebraiska notationen och kvantkretsdiagrammen.

Indata och utdata från kvantkretsar

I ett kvantkretsdiagram representerar kablarna som går in i en kvantgrind de kvantbitar som matas in till kvantgrinden, och kablarna som lämnar kvantgrinden representerar de kvantbitar som matas ut från kvantgrinden.

Antalet indata för en kvantgrind är lika med antalet utdata från en kvantgrind. Det beror på att kvantåtgärder är enhetliga och därmed reversibla. Om en kvantgrind hade fler utdata än indata skulle den inte vara reversibel och därmed inte enhetlig, vilket är en motsägelse.

Av den anledningen måste alla rutor som ritas i ett kretsdiagram ha exakt samma antal ledningar som går in i den som när den avslutas.

Multi-qubit-åtgärder

Diagram med flera kvantbitar följer liknande konventioner som enstaka kvantbitsdiagram. Till exempel kan en enhetsåtgärd $med två kvantbitar B$ definieras som $(H S\otimes X)$, så motsvarande kvantkrets är följande:

Du kan också se $B$ som att ha en åtgärd på ett enda två-qubit-register i stället för två en-qubit-register beroende på kontexten där kretsen används.

Den kanske mest användbara egenskapen för sådana abstrakta kretsdiagram är att de tillåter att komplicerade kvantalgoritmer beskrivs på hög nivå utan att behöva kompilera dem ner till grundläggande grindar. Det innebär att du kan få en intuition om dataflödet för en stor kvantalgoritm utan att behöva förstå all information om hur var och en av subrutinerna i algoritmen fungerar.

Kontrollerade portar

Kvantstyrda grindar är två qubitgrindar som tillämpar en grind med en kvantbit på en target kvantbit om en kontrollkvabit är i ett specifikt tillstånd.

Tänk dig till exempel en kvantkontrollerad $\Lambdagrind, som anges (G)$, där en enda kvantbits värde styr tillämpningen av $G-åtgärden$ . Den kontrollerade grinden $\Lambda(G)$ kan förstås genom att titta på följande exempel på produkttillståndsindata:

$\Lambda(G) (\alpha\ket{{0} + \beta\ket{1}) \ket{\psi}\alpha\ket{\psi}\ket{{0}=+ G \beta\ket{{1}\ket{\psi}$

Det vill säga, den kontrollerade grinden tillämpar $G$ på registret som innehåller $\psi$ om och endast om kontrollkvabiten tar värdet $1$. I allmänhet beskrivs sådana kontrollerade åtgärder i kretsdiagram med följande symbol:

Här anger den svarta cirkeln kvantbiten som grinden styrs på och en lodrät tråd anger den enhetliga som tillämpas när kontrollkvabiten tar värdet $1$.

För de särskilda fall där $G=X$ och $G=Z$ används följande notation för att beskriva den kontrollerade versionen av grindarna (observera att den kontrollerade X-grinden är CNOT-grinden):

Q# tillhandahåller metoder för att automatiskt generera den kontrollerade versionen av en åtgärd, vilket sparar programmeraren från att behöva handkoda dessa åtgärder. Ett exempel på detta visas nedan:

operation PrepareSuperposition(qubit : Qubit) : Unit
is Ctl { // Auto-generate the controlled specialization of the operation
    H(qubit);
}

Klassiskt kontrollerade grindar

Kvantgrindar kan också användas efter en mätning, där resultatet av mätningen fungerar som en klassisk kontrollbit.

Följande symbol representerar en klassiskt kontrollerad grind, där $G$ tillämpas villkorat på att den klassiska kontrollbiten är värde $1$:

Måttoperator

Mätningsåtgärder tar ett kvantbitsregister, mäter det och matar ut resultatet som klassisk information.

En mätningsåtgärd betecknas med en mätarsymbol och tar alltid som indata ett qubitregister (som anges av en fast linje) och utdata klassisk information (som anges av en dubbel linje). Mer specifikt ser måttåtgärdens symbol ut så här:

I Q#implementerar operatorn Measure mätningsåtgärden.

Exempel: Enhetlig transformering

Överväg den enhetliga omvandlingen $\text{ CNOT}_{01}(H\otimes 1)$. Den här grindsekvensen är av grundläggande betydelse för kvantberäkning eftersom den skapar ett maximalt sammanflätat två-qubit-tillstånd:

$\mathrm{CNOT}_{01}(H\otimes 1)\left=\ket{00}\frac{1}{\sqrt{2}}({00}\ket{ + ), \ket{11}\right$

Åtgärder med den här eller större komplexiteten är allestädes närvarande i kvantalgoritmer och kvantfelkorrigering.

Kretsdiagrammet för att förbereda det här maximalt sammanflätade kvanttillståndet är:

Symbolen bakom Hadamard-grinden representerar en CNOT-grind, där den svarta cirkeln indikerar kontrollkvabiten och korset i en cirkel indikerar kvantbiten target . Den här kvantkretsen visas som agerar på två kvantbitar (eller motsvarande två register som består av en qubit).

Exempel: Diagram över teleporteringskretsar

Kvantteleportering är en av de bästa kvantalgoritmerna för att illustrera kretskomponenter.

Kvantteleportering är ett protokoll som gör att ett kvanttillstånd kan överföras från en kvantbit till en annan, med hjälp av ett delat sammanflätat tillstånd mellan avsändaren och mottagaren, och klassisk kommunikation mellan dem.

I utbildningssyfte kallas avsändaren Alice, mottagaren heter Bob och kvantbiten som ska teleporteras kallas för meddelandekvenbiten. Alice och Bob har en qubit vardera, och Alice har en extra qubit som är meddelandets qubit.

Följande kretsdiagram illustrerar teleporteringsprotokollet:

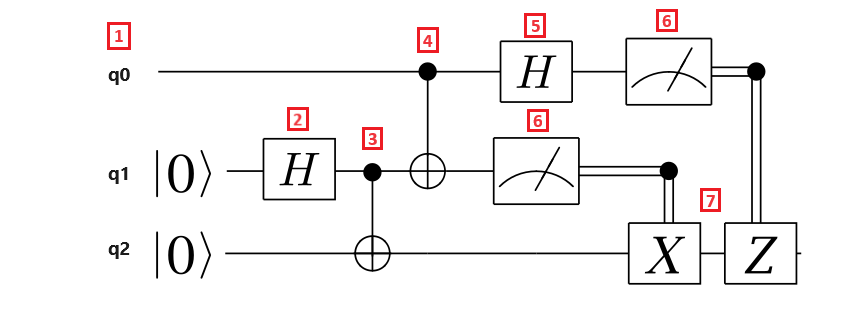
Nu ska vi gå igenom stegen i teleporteringsprotokollet:

1. Qubit register q0 är meddelandet qubit, qubit register q1 är Alice qubit och qubit register q2 är Bobs qubit. Meddelandekvabiten är i ett okänt tillstånd och Alice och Bobs kvantbitar är i tillståndet $\ket{0}$ .
2. En Hadamard-grind tillämpas på Alice qubit. Eftersom kvantbiten $\ket{0}$ är i tillståndet är $\frac{1}{\sqrt{{2}}det resulterande tillståndet (\ket{{0} + \ket{1})$.
3. En CNOT-grind tillämpas på Alice och Bobs kvantbitar. Alice qubit är kontrollkvabiten och Bobs qubit är qubiten target . Det resulterande tillståndet är $\frac{{1}{\sqrt{2}}(\ket{00} + \ket{{11})$. Alice och Bob delar nu ett sammanflätat tillstånd.
4. En CNOT-grind tillämpas på meddelandets qubit och Alice qubit. Eftersom Alices qubit också är sammanflätad med Bobs qubit är det resulterande tillståndet ett sammanflätat tillstånd med tre kvantbitar.
5. En Hadamard-grind tillämpas på meddelandets qubit.
6. Alice mäter sina två kvantbitar och berättar mätresultatet för Bob, som inte återspeglas i kretsen. Mätresultaten är två klassiska bitar som kan ta värdena 00, 01, 10 eller 1
7. Två klassiskt kontrollerade Pauli-portar X och Z tillämpas på Bobs qubit, beroende på att resultatbiten är värde $1$. Det resulterande tillståndet är det ursprungliga meddelandets qubit-tillstånd.

Relaterat innehåll

• Kvantsammanflätning
• Grover-algoritm
• Mellanliggande kvantrepresentation
• Vektorer och matriser