Co je superpozice v kvantových výpočtech?

Dokončeno

V klasickém světě mohou skutečné objekty jako kočka a krabice být pouze v jednom stavu najednou. V kvantovém světě ale částice mohou existovat v superpozici všech možných stavů.

Bohužel neexistují žádné kvantové počítače, které k provádění výpočtů používají kočky. Místo toho skutečné kvantové počítače používají qubity, zkratky pro kvantové bity. Stejně jako to, jak je bit základní jednotkou informací v klasickém computingu, je qubit základní jednotkou informací v kvantovém computingu. Stejně jako to, jak můžou bity vzít jednu ze dvou možných hodnot, 0 a 1, má qubit také hodnotu 0 nebo 1, když ho změříme.

Existuje mnoho fyzických reprezentací qubitů. Například polarizace fotonu nebo rotace elektronu lze použít jako qubity, protože fotony mají dva odlišné polarizační stavy a elektrony mají při měření dva různé spinové stavy. Můžeme reprezentovat jeden z těchto stavů jako 0 a druhý stav jako 1, a qubit bude vždy dávat 0 nebo 1, když ho změříme.

Jak ale představujeme superpozici v qubitu? A jaká je pravděpodobnost, že při měření zjistíme, že qubit bude v určitém stavu?

Reprezentace Blochovy sféry superpozice pro jednotlivé qubity

Qubit je kvantová částice, která je v jednom ze dvou možných stavů při měření qubitu. Bez ohledu na fyzickou povahu qubitu označíme oba stavy jako 0 a 1. Qubit může být ve stavu 0, ve stavu 1 nebo v nekonečném počtu superpozic stavů 0 i 1. Jak tyto superpozice představujeme v kvantových výpočtech?

Užitečné geometrické znázornění stavu superpozice jednoho qubitu je Bloch sphere.

Představte si, že kreslete kruh s poloměrem jednotky (délka poloměru rovna 1). Potom nakreslete svislou a vodorovnou osu tak, aby se obě osy protínaly uprostřed kruhu. Teď nadefinujme stav 0, ve kterém svislá osa odpovídá horní části kruhu, a 1 stav, ve kterém svislá osa odpovídá dolní části kruhu. Na tomto kruhu jsou stavy 0 a 1 od sebe navzájem vzdáleny o $180^\circ$, nebo $\pi$ radiánů.

Jak tato reprezentace souvisí se stavem qubitu? Můžeme znázorňovat stav qubitu pomocí šipky (nebo vektoru) délky jednotky, která je nakreslena ze středu kruhu na okraj kruhu. Když vektor směřuje svisle nahoru, qubit je ve stavu 0 a když vektor směřuje svisle dolů, qubit je ve stavu 1. V této reprezentaci by klasický bit byl vektor, který vždy ukazuje rovnou nahoru nebo rovnou dolů, ale nikdy v žádném jiném směru.

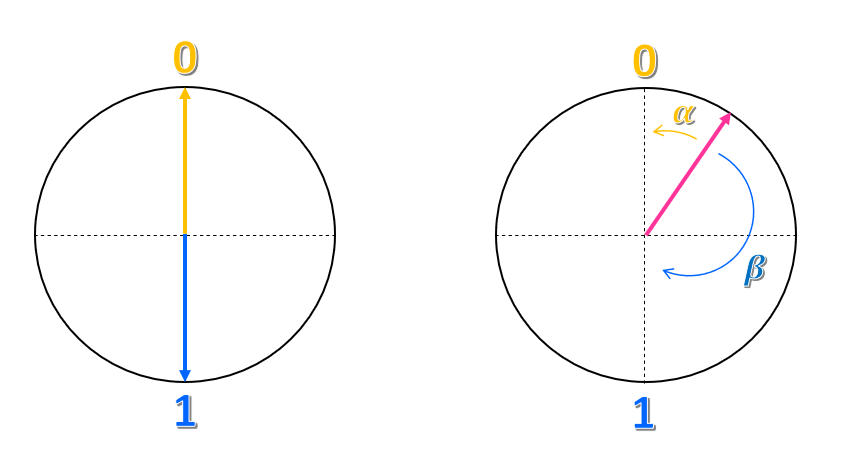
U qubitu může vektor nasměrovat na libovolné místo v kruhu. Každé umístění v kruhu, které není rovnou nahoru nebo rovnou dolů, představuje stav superpozice. Například nazýváme úhel, který vektor dělá se stavem 0 $\alpha$ a úhel, který vektor dělá s 1 stavem $\beta$. Pak představujeme stav superpozice qubitu jako $\alpha 0 + \beta 1$.

Podobně jako v příkladu kočky a rámečku je superpozice stavu qubitu součtem jednotlivých stavů, 0 a 1, váženými čísly $\alpha$ a $\beta$. V systému cat-and-box jsou však váhy skutečnými čísly, ale v qubitovém systému jsou váhy $\alpha$ a $\beta$ komplexní čísla.

Vzhledem k tomu, že amplitudy $\alpha$ a $\beta$ jsou komplexní čísla, potřebujeme další kruh v našem diagramu, který je v rovině kolmém k prvnímu kruhu, aby skutečně představoval jakýkoli stav superpozice qubitu. Tyto dva kruhy existují ve třech dimenzích pro výrobu Bloch sphere.

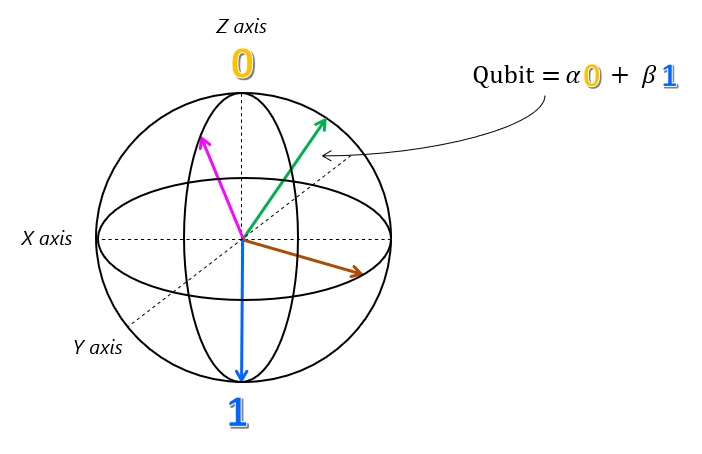
Tato blochová koule je přesná geometrická reprezentace každého možného stavu superpozice pro jeden qubit. Stav qubitu je reprezentován umístěním na povrchu sféry, na které vektor ukazuje. Stejně užitečná jako Blochova sféra bohužel nelze rozšířit na systémy s více qubity.

Návod

Bloch sphere je výkonný nástroj, protože operace, které provádíme na qubitu během kvantového výpočtu, jsou reprezentovány jako rotace o jedné z kardinalních os Blochovy sféry. Tato geometrická reprezentace pomáhá vytvářet intuitivní informace o tom, jak operace fungují v kvantových výpočtech, ale je náročné tuto intuici použít k návrhu a popisu algoritmů. Jazyk Q# pomáhá tím, že poskytuje prostředky pro popis těchto rotací.

Jaká je pravděpodobnost nalezení qubitu v určitém stavu?

V systému kočka-a-krabice z předchozí jednotky jsou váhy pro každý stav čísla, která přímo vyjadřují pravděpodobnost, s jakou systém najdeme v jednotlivých stavech. V qubitovém systému jsou čísla $\alpha$ a $\beta$ obecně komplexní čísla, která přímo neudělují pravděpodobnosti nalezení qubitu ve stavech 0 a 1. Místo toho se tato čísla označují jako amplitudy pravděpodobnosti (nebo jen amplitudy).

Skutečné pravděpodobnosti se počítají z mocnin velikostí amplitud pravděpodobnosti. Pravděpodobnost, že měření najde qubit ve stavu 0, je $|\alpha|^2$ a pravděpodobnost, že měření najde qubit ve stavu 1, je $|\beta|^2$. Obecně $\alpha + \beta$ nesčítá na 100 %, ale $|\alpha|^2 + |\beta|^2$ vždy ano. Omezení, které $|\alpha|^2 + |\beta|^2 = 1$ se nazývá podmínka normalizace a každý platný kvantový stav musí splňovat tuto podmínku.