Dirac-jelölés

A dirac jelölés egy olyan nyelv, amely a kvantummechanikában az állapotok kifejezésének pontos igényeihez igazodik. A cikkben szereplő példák olyan javaslatok, amelyek a kvantumötletek tömör kifejezésére használhatók.

Az oszlopvektor jelölésének korlátozásai

Bár az oszlopvektor-jelölés gyakori a lineáris algebrában, a kvantum-számítástechnikában gyakran nehézkes, különösen több qubit kezelése esetén. Ha például egy vektort határoz meg $\psi$ , az nem egyértelmű egyértelműen, hogy sor vagy oszlopvektor-e $\psi$ . Így, ha $\phi$ és $\psi$ vektorok, akkor egyformán nem egyértelmű, ha $\phi\psi$ még meg is határozták, mert a és $\psi$ az alakzatai $\phi$ nem egyértelműek a kontextusban. A vektorok alakzatainak kétértelműségén túl a lineáris algebrai jelölést használó egyszerű vektorok kifejezése is nehézkes lehet. Ha például egy $n-qubit$ állapotot szeretne leírni, ahol minden qubit a 0$ értéket $veszi fel, akkor formálisan az állapotot

$$\begin{bmatrix}1 \\ 0 \end{bmatrix}\otimes\otimes\begin{bmatrix}\cdots1 \\ 0 .\end{bmatrix} $$

A tenzortermék kiértékelése nem praktikus, mert a vektor exponenciálisan nagy térben helyezkedik el. Ezért ez a jelölés valójában az előző jelöléssel adható állapot legjobb leírása.

Vektortípusok a Dirac-jelölésben

A Dirac-jelölésben kétféle vektor létezik: a bra vektor és a ket vektor, így elnevezve, mert ha össze vannak adva, akkor egy fékező vagy belső terméket alkotnak. Ha $\psi$ egy oszlopvektor, akkor dirac jelöléssel $\ket{\psi}$is megírhatja, ahol a $\ket{\cdot}$ azt jelzi, hogy egy egységoszlopvektor, például egy ket vektor. Hasonlóképpen a(z) ^\dagger$ sorvektor $\psia következőként $\bra{\psi}$van kifejezve: . Más szóval a $\psi^\dagger$ a transzponálás elemeinek beviteli szempontból összetett konjugációjának alkalmazásával érhető el $\psi$. A bra-ket jelölés közvetlenül azt jelenti, hogy $\braket{\psi|\psi}$ a vektor $\psi$ belső szorzata önmagával, amely definíció szerint $1$.

Általánosabban, ha $\psi$ és $\phi$ kvantumállapot-vektorok, akkor a belső termékük a $\braket{\phi|\psi}$. Ez a belső termék azt jelenti, hogy az állapot $\ket{\psi}$ mérésének $\ket{\phi}$$|\braket{\phi|\psi}|valószínűsége ^2$.

A következő konvenció a nulla és egy (egy qubites számítási alapállapotok) értékeit kódoló kvantumállapotok leírására szolgál:

$$\begin{bmatrix}1 \\ 0 \end{bmatrix}{0}\ket{=,\qquad\begin{bmatrix} 0 \\ 1 .\end{bmatrix}=\ket{{1} $$

Példa: A Hadamard-művelet dirac jelöléssel való ábrázolása

A következő jelölést gyakran használják a Hadamard-kapu és $\ket{1}$az -ra való alkalmazásából eredő állapotok leírására$\ket{0}$. Ezek az állapotok a Bloch-gömb +x$ és $-x$ irányában $lévő egységvektoroknak felelnek meg:

$$\frac{1}{\sqrt{{2}}\begin{bmatrix}1 \\ 1 \end{bmatrix}=H\ket{=\ket{0}+},\qquad\frac{1}{\sqrt{{2}}\begin{bmatrix} 1 \\ -1=\end{bmatrix} H .\ket{{1}=\ket{{-} $$

Ezek az állapotok dirac jelöléssel is kibonthatók a és $\ket{1}$összegeként$\ket{0}$:

$$\ket{+}={1}{\sqrt{2}}\frac{(\ket{0} + \ket{1}),\qquad\frac{={1}{\sqrt{\ket{{2}}{-}(\ket{{0} - ). \ket{1} $$

Számítási alapvektorok

Ez azt mutatja be, hogy miért nevezik ezeket az állapotokat gyakran számítási alapnak: minden kvantumállapot mindig számítási alapvektorok összegeként fejezhető ki, és az ilyen összegek egyszerűen kifejezhetők Dirac-jelöléssel. A converzum abban is igaz, hogy az állapotok $\ket{+}$ és $\ket{-}$ a kvantumállapotok alapjául is szolgálnak. Ez abból a tényből látható, hogy

$$\ket{{0}=\frac{1}{\sqrt{2}}(\ket{+} + \ket{-}),\qquad\frac{{1}{\sqrt{=\ket{{1}{2}}(\ket{+} - ). \ket{-} $$

A Dirac jelölésére példaként vegyük a fékező $\braket{0 | 1-et}$, amely a 0$ és $1$ közötti $belső termék. A következőképpen írható:

$$\braket{0 | 1}=\begin{bmatrix} 1 & 0 \end{bmatrix}\begin{bmatrix}0\\ 1\end{bmatrix}=0. $$

Ez a példa azt mondja, hogy $\ket{{0}$ és $\ket{{1}$ ortogonális vektorok, ami azt jelenti, hogy $\braket{0 | 1 1\braket{=|} 0 0.}=$ Emellett a 0 0 | 1=}\braket{1 | 1}=$ definíció $\braket{szerint ez azt jelenti, hogy a két számítási alapvektort ortonormálisnak is nevezhetjük.

Az alábbi példában ezeket az ortoporális tulajdonságokat használjuk. Ha az állapota $\ket{\psi}{1}=\ket{{\frac{3}{5}}+{4}{5}}\ket{0}${\frac{ , akkor mivel $\braket{az 1 | 0 0=$} az 1$ mérésének valószínűsége $

$$\big|\braket{1 |^2\left|\frac{{3}{5}\braket{=1 | 1} +\frac{{4}{5}\braket{1 | 0}\right|^2{25}=\frac{{9}{.\psi}\big| $$

Tensor termék jelölése

A dirac jelölés egy implicit tenzoros termékstruktúrát is tartalmaz. Ez a struktúra azért fontos, mert a kvantum-számítástechnikában a két nem korrelált kvantumregisztrációs regiszter által leírt állapotvektor a két állapotvektor tenzorterméke. A tenzoros termékstruktúra tömör leírása, vagy annak hiánya elengedhetetlen, ha egy kvantumszámítást szeretne elmagyarázni. A tenzoros termékstruktúra azt jelenti, hogy bármelyik két kvantumállapot-vektorhoz $\phi$ írhat$\psi\otimes\phi$, és $\psi$ mint .$\ket{\psi}\otimes\ket{\phi}$ Azonban konvenció szerint a vektorok közötti írás $\otimes$ szükségtelen, és megírhatja a következőt\ket{\psi$$\ket{\psi}\ket{\phi}=\phi}: . A vektorokról és a tenzortermékekről további információt a Vektorok és mátrixok a Kvantum-számítástechnikában című témakörben talál. A nulla állapotba inicializált két qubitet tartalmazó állapot például a következő:

$$\ket{0}\otimes\ket{0}=\ket{{0}\ket{{0}=\ket{{00}=\begin{bmatrix}1 \\ 0\otimes\end{bmatrix}\begin{bmatrix} 1 \\ 0 \end{bmatrix}=\begin{bmatrix} 1 \\ 0 \\ 0 \\ 0 .\end{bmatrix} $$

Hasonlóképpen, a p$ egész szám p $}$ állapota $\ket{egy kvantumállapotot jelöl, amely bináris ábrázolásban kódolja a p egész számot$$. Ha például egy aláíratlan bináris kódolással szeretné kifejezni az 5-ös$ számot$, ugyanúgy kifejezheti, mint

$$\ket{1}\ket{0}\ket{1}=\ket{101}=\ket{5}. $$

Ebben a jelölésben nem egy qubites állapotra kell hivatkoznia, $\ket{0}$ hanem egy 0$ bináris kódolást tároló qubit-regiszterre$. A két jelölés közötti különbségek egyértelműek a kontextusból. Ez a konvenció az első példa egyszerűsítése érdekében hasznos, amely az alábbi módokon írható:

$$\begin{bmatrix}1 \\ 0\cdots\otimes\begin{bmatrix}\end{bmatrix}\otimes 1 \\ 0 0{0}\ket{\otimes\cdots|\otimes\ket{0}==\end{bmatrix} 0\cdots=\ket{\rangle{0}^ n{\otimes}$$

ahol $\ket{0}a ^{\otimes n}$ az n$$\ket{0}$ kvantumállapotok tensor szorzatát $jelöli.

Példa: A szuperpozíció leírása Dirac jelöléssel

Egy másik példa arra, hogyan használható a Dirac-jelölés egy kvantumállapot leírására, vegye figyelembe az alábbi egyenértékű módszereket egy olyan kvantumállapot írására, amely egyenlő szuperpozíció minden lehetséges n hosszúságú $bitsztring felett$

$$H^{\otimes n}=\frac{1}{\ket{0}2^{n/2\sum}}_{j=0}^{2^n-1\ket{}j}=\ket{+}^{\otimes n.} $$

Itt felmerülhet a kérdés, hogy $az összeg miért 0$ és $2^{n-1$} között $van n$ bit esetén. Először is vegye figyelembe, hogy $az n$ bitek 2^{n}$ különböző konfigurációt $használhatnak. Ezt úgy tekintheti meg, hogy egy bit 2$ értéket vehet fel$, de két bit 4$ értéket és $így tovább. Ez általában azt jelenti, hogy 2^n$ különböző lehetséges bitsztring van$, de a legnagyobb kódolt érték bármelyikben $1 1\cdots= 2^n-1$, ezért ez az összeg felső korlátja. Mellékes megjegyzésként ebben a példában nem használta $\ket{a +}^{\otimes n+}$ függvényt a$\ket{{0}^{\otimesn\ket{}=\ket{}={0}$ hasonlatában. Ez a jelölési konvenció a számítási alapállapot számára van fenntartva, és minden qubit nullára van inicializálva. Bár egy ilyen konvenció ebben az esetben ésszerű, a kvantum-számítástechnika szakirodalmában nem alkalmazzák.

Lineárisság kifejezése Dirac-jelöléssel

A Dirac-jelölés egy másik jellemzője az a tény, hogy lineáris. Például két komplex számhoz $\alpha$ és $\beta$.

$$\ket{\psi}\otimes ( \alpha\ket{\phi} + \beta\ket{\chi})=\alpha\ket{\psi}\ket{\phi} + \beta\ket{\psi}\ket{\chi}.$$

Ez azt jelzi, hogy a tenzor termék jelölését dirac jelölésben eloszthatja úgy, hogy a tenzortermékeket az állapotvektorok között a szokásos szorzáshoz hasonlóan kell kivenni.

A bra vektorok a ket vektorokhoz hasonló konvekciót követnek. A vektor $\bra{\psi}\bra{\phi}$ például egyenértékű a(z) ^\otimes\phi\dagger^\dagger=(\psi\otimes\phi)^állapotvektorral.$\psi\dagger$ Ha a ket vektor $\ket{\psi}$$\alpha\ket{0} + \beta\ket{1}$, akkor a vektor kapcsos vektorának $\bra{\psi}=\ket{\psi}verziója ^\dagger= ({0}\alpha\bra{^* +\bra{1}\beta^*).$

Tegyük fel például, hogy ki szeretné számítani az állapot $\ket{\psi}\frac{3}{5}=\ket{{1} mérésének valószínűségét + \frac{4}{5}\ket{0}$ egy kvantumprogrammal, amellyel az állapotok $\ket{mérése +}$ vagy .$\ket{{-}$ Ezután annak a valószínűsége, hogy az eszköz kimenete az állapot $\ket{-}$

$$|\braket{- |^2\left|\frac{={1}{\sqrt{{2}}(\bra{0} -{1}\bra{ )(\frac{3}{5}{1}\ket{ +{4}{5}\frac{\ket{0} ) \right|^2-5=\left|{2}}\frac{3}{\sqrt{ +{4}{\frac{ 5\sqrt{2}}\right|^2.=\frac{{1}{{50}\psi}|$$

Az a tény, hogy a negatív jel megjelenik a valószínűség kiszámításában, a kvantum-interferencia megnyilvánulása, amely az egyik olyan mechanizmus, amellyel a kvantum-számítástechnika előnyt szerez a klasszikus számítástechnikával szemben.

ketbra vagy külső termék

Az utolsó tétel érdemes megvitatni a Dirac jelölés a ketbra vagy a külső termék. A külső termék dirac jelölésekben $\ket{\psi}\bra{\phi}$, és néha ketbrának is nevezik, mert a melltartók és a ketek ellentétes sorrendben fordulnak elő fékezésként. A külső termék a mátrix szorzásán keresztül van meghatározva^ értékként $\ket{\psi}\psi=\phi\bra{\phi}a kvantumállapot-vektorok $\psi$ és $\phi$a esetében.\dagger$ Ennek a jelölésnek a legegyszerűbb és vitathatatlanul leggyakoribb példája a következő:

$$\ket{0}\bra{{0}=\begin{bmatrix}1\\ 0 \end{bmatrix}\begin{bmatrix}1& 0 \end{bmatrix}=\begin{bmatrix}1 & 0\\ 0 & 0\end{bmatrix}\bra{1}=\qquad\ket{1}\begin{bmatrix}0\\ 1 \end{bmatrix}\begin{bmatrix}0& 1 \end{bmatrix}=\begin{bmatrix}0 & 0\\ 0 & 1\end{bmatrix}. $$

A Ketbrákat gyakran projektoroknak is nevezik, mert kvantumállapotokat vetnek egy rögzített értékre. Mivel ezek a műveletek nem egységesek (és nem is őrzik meg a vektorok normát), a kvantumszámítógépek nem alkalmazhatnak determinisztikusan kivetítőt. A kivetítők azonban gyönyörűen írják le azt a műveletet, amelyet a mérés a kvantumállapotban végez. Ha például egy állapotot $\ket{\psi}$ 0-ra $$mér, akkor az eredményként kapott átalakítás, amelyet az állapot a mérés eredményeként tapasztal

$$\ket{\psi}\rightnyíl \frac{(\ket{{0}\bra{{0})\ket{\psi}}{|\braket{0 ,|\psi}|}=\ket{{0}$$

ahogy azt várta, ha az állapotot mérte, és a következőt $\ket{0}$találta: . Megismétlem, az ilyen kivetítők nem alkalmazhatók kvantumszámítógépek állapotára determinisztikus módon. Ehelyett a legjobb esetben véletlenszerűen alkalmazhatók, ha az eredmény $\ket{0}$ bizonyos rögzített valószínűséggel jelenik meg. Az ilyen sikeres mérések valószínűsége megírható a kvantumprojektor várható értékeként az állapotban

$$\bra{\psi}(\ket{0}\bra{0})\ket{\psi}|=|\braket{\psi 0}|^2,$$

amely azt mutatja be, hogy a kivetítők új módot adnak a mérési folyamat kifejezésére.

Ha ehelyett egy több qubites állapot első qubitjének mérését 1-nek $$tekinti, akkor ezt a folyamatot kényelmesen leírhatja kivetítőkkel és Dirac jelöléssel:

$$P(\text{első qubit = 1})=\bra{\psi}\left(\ket{{1}\bra{{1}\otimes \mathbf{\mathbf{1}^{\otimes n-1}\right) . \ket{\psi} $$

Itt az identitásmátrix kényelmesen megírható Dirac-jelölésként

$$\mathbf{1}=\ket{0}\bra{0}+\ket{1}\begin{bmatrix}\bra{{1}=1& 0\\ 0& 1 \end{bmatrix}. $$

Abban az esetben, ha két qubit van, a kivetítő kibontható

$$\ket{1}\bra{1}\otimes\id=\ket{{1}\bra{1}\otimes(\ket{{0}{0}\bra{+\ket{1}{1}\bra{)={10}\ket{10}\bra{ + . \ket{{11}\bra{{11} $$

Ezután láthatja, hogy ez összhangban van a többkettős állapotok oszlopvektor-jelölést használó mérési valószínűségével kapcsolatos vitával:

$$P(\text{első qubit = 1})\psi=^\dagger (e_{10}e_{10}^\dagger + e_{{11}e_{11}{^\dagger)|\psi=e_{10}{^\psi|\dagger^2 + |e_{11}^\dagger\psi|^2,$$

amely megfelel a több qubites mérési vitafórumnak. Ennek az eredménynek a multi-qubites esetre történő általánosítása azonban valamivel egyszerűbb a Dirac-jelöléssel való kifejezéshez, mint az oszlopvektor-jelölés, és teljes mértékben egyenértékű az előző kezeléssel.

Sűrűség operátorok

Egy másik hasznos operátor a Dirac-jelölés használatával történő kifejezéshez a sűrűség operátor, más néven állapotoperátor. A kvantumállapot-vektorként a sűrűségoperátor egy rendszer kvantumállapotát írja le. Bár a kvantumállapot-vektorok csak tiszta állapotokat képviselhetnek, a sűrűségoperátorok vegyes állapotokat is képviselhetnek.

Általánosságban elmondható, hogy egy adott \rho$ mátrix $érvényes sűrűségoperátor, ha a következő feltételek teljesülnek:

• $A \rho$ összetett számok mátrixa
• $\rho = \rho^{\dagger}$ (azaz $\rho$ remitianus)
• Minden eigenvalue $p$ \ $rho$ értéke $0 <= p <= 1$
• A \rho$ összeg összes eigenvalues értéke $1-nek

Ezek a feltételek együttesen garantálják, hogy $a \rho$ együttesnek tekinthető. A kvantumállapot-vektor $\ket{\psi}$ sűrűségi operátora a \rho\sum= _i p_i \ket{\psi_i\bra{\psi}_i}$$a \rho$ eigenvalue felbontása$, majd $a \rho$ a \rho{=\ket{\psi _i}\text{együttest $írja le valószínűségi} p_i.}$

A tiszta kvantumállapotok azok, amelyeket egyetlen ketvektor vagy hullámfüggvény jellemez, és nem írhatók más kvantumállapotok statisztikai keverékeként (vagy konvex kombinációjáként). A vegyes kvantumállapot a tiszta állapotok statisztikai együttese.

A Bloch-gömbön a tiszta állapotokat a gömb felszínén lévő pont jelöli, míg a vegyes állapotokat egy belső pont képviseli. Egy qubit vegyes állapotát a gömb középpontja, szimmetria jelöli. Az állapot tisztasága úgy jeleníthető meg, mint az a fok, amelyben közel van a gömb felszínéhez.

Az állapot mátrixként való ábrázolásának ez a fogalma gyakran kényelmes, mivel kényelmes módot ad a valószínűségszámítások megjelenítésére, és lehetővé teszi a statisztikai bizonytalanság és a kvantumbizonytalanság leírását is ugyanazon a formalizmuson belül.

Tipp

A QuTiP-kódtár hasznos Python-kódtár a kvantumállapotok használatakor. A kvantumállapotokat QuTiP-jelöléssel írhatja, a qt.basis(2, i) használatával pedig i-t}$ jelölhet $\ket{egyetlen qubiten. A QuTiP-módszerekkel és -funkciókkal kapcsolatos további információkért lásd a QuTiP felhasználói útmutatóját.

A \rho$ sűrűségoperátor $tiszta állapotot jelöl, ha és csak akkor, ha:

• $A \rho egy \rho$ állapotvektor $külső termékeként írható=\ket{\psi}\bra{\psi}$
• $\rho =\rho^2$
• $tr(\rho^2)=1$

Annak megállapításához, hogy egy adott sűrűségoperátor $(\rho$) milyen közel van ahhoz, hogy tiszta legyen, megnézheti a \rho^2$ nyomvonalát $(azaz az átlós elemek összegét). A sűrűségoperátor tiszta állapotot jelöl, ha és csak akkor, ha $tr(\rho ^{2})=1$.

Vegye figyelembe a \rho_mixed( \ket{0}\bra{0} + \ket{1}\bra{{1}\right)$, vegyes állapotot{1}{2}\left=$}}\frac{.{\text{

import qutip as qt

ket0 = qt.basis(2, 0)
ket1 = qt.basis(2, 1)

rho_mixed = (ket0 * ket0.dag() + ket1 * ket1.dag()) / 2
print(rho_mixed)

Quantum object: dims = [[2], [2]], shape = (2, 2), type = oper, isherm = True
Qobj data =
[[0.5  0.0]
 [0.0  0.5]]

A \rho nyomkövetése $Tr(\rho)$ néven $van megírva, és a QuTiP metódusával .tr() számítható ki:$

print((rho_mixed ** 2).tr())

0.5

Most tekintsük át a tiszta kvantumállapotot \rho_{\text{pure}}=\ket{++}\bra{}$,$

ket_plus = (1 / np.sqrt(2)) * (ket0 + ket1)
rho_pure = ket_plus * ket_plus.dag()
print(rho_pure)

Quantum object: dims = [[2], [2]], shape = (2, 2), type = oper, isherm = True
Qobj data =
[[0.5  0.5]
 [0.5  0.5]]

A(z) $\rho_{\text{pure}}^2$ nyomkövetése a következő:

print((rho_pure ** 2).tr())

0.9999999999999996

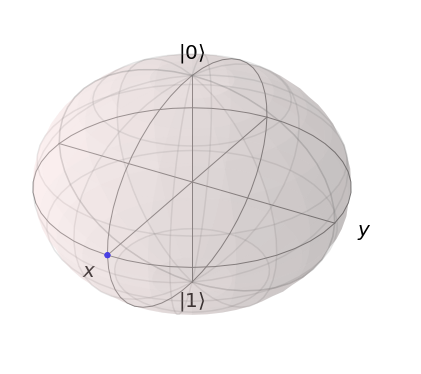
Egy qubites rendszerek esetén a vegyes állapotok ugyanúgy ábrázolhatók a Bloch-gömbön, mint az állapotvektorok – így a tiszta állapotok azok az állapotok, amelyek a Bloch-gömb felszínén fekszenek, míg a vegyes állapotok általában idézhetők &; belső&idézőjel; a Bloch-gömb.

import matplotlib.pyplot as plt

plt.figure(figsize=(6, 6))
bloch = qt.bloch.Bloch()
bloch.add_states([rho_pure], kind='point')
print(bloch.show())

plt.figure(figsize=(6, 6))
bloch = qt.bloch.Bloch()
bloch.add_states([rho_mixed], kind='point')
bloch.show()

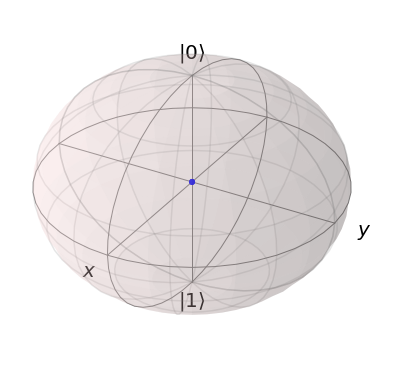
A Bloch-gömb közepén lévő állapot a maximálisan vegyes állapot. A tiszta állapotoktól eltérően a maximálisan vegyes állapot 50/50 eredményt ad vissza az ideális Pauli-mérésekhez.

Q# kvantumállapotokkal egyenértékű kapuütemezések

Egy utolsó pont, amelyet érdemes kiemelni a kvantum jelöléséről és a Q# programozási nyelvről: a dokumentum elején említettük, hogy a kvantumállapot a kvantum-számítástechnika alapvető információobjektuma. Meglepő lehet, hogy Q# a kvantumállapot fogalma nem létezik. Ehelyett minden állapotot csak az előkészítéshez használt műveletek írnak le. Az előző példa ennek kiváló illusztrációja. Ahelyett, hogy egységes szuperpozíciót ad meg egy regiszter minden kvantumbitsztringje felett, az eredményt H^{\otimes n}\ket{0}$ értékként $jelölheti. Az állapot exponenciálisan rövidebb leírása nem csupán azzal az előnnyel jár, hogy ezt klasszikusan meg lehet indokolni, hanem tömören meghatározza azokat a műveleteket is, amelyeket az algoritmus implementálásához a szoftververemen keresztül kell propagálni. Ezért úgy tervezték, Q# hogy kvantumállapotok helyett kapuütemezéseket bocsát ki; elméleti szinten azonban a két perspektíva egyenértékű.

Következő lépések

• Pauli-mérések
• T-kapuk és T-gyárak
• Kvantumkörök
• Kvantumorákulumok