Dela via

Kvantbiten i kvantberäkning

Precis som bitar är det grundläggande objektet för information inom klassisk databehandling är kvantbitar (kvantbitar) det grundläggande informationsobjektet inom kvantberäkning. För att förstå den här korrespondensen tittar den här artikeln på det enklaste exemplet: en enda qubit.

Representerar en qubit

Medan en bit, eller en binär siffra, kan ha ett värde antingen 0 eller 1, kan en kvantbit ha ett värde som är antingen $0$, $1$ eller en kvantsuperposition på $0$ och $1$.$$$$

Tillståndet för en enda kvantbit kan beskrivas med en tvådimensionell kolumnvektor av enhetsnorm, det vill säga att summan av kvadraterna av dess element måste vara $1$. Den här vektorn, som kallas kvanttillståndsvektor, innehåller all information som behövs för att beskriva kvantsystemet med en kvantbit precis som en enda bit innehåller all information som behövs för att beskriva tillståndet för en binär variabel. Grunderna i vektorer och matriser inom kvantberäkning finns i Vektor och matriser.

Alla tvådimensionella kolumnvektorer med verkliga eller komplexa tal med norm $1$ representerar ett möjligt kvanttillstånd som innehas av en kvantbit. Representerar således $\begin{bmatrix}\alpha\\\beta\end{bmatrix}$ ett qubit-tillstånd om $\alpha$ och $\beta$ är komplexa tal som uppfyller $|\alpha|^2 + |\beta|^2 = 1.$

Några exempel på giltiga kvanttillståndsvektorer som representerar kvantbitar är $\begin{bmatrix} 1 \\ 0 \end{bmatrix}$ och $\begin{bmatrix} 0 \\ 1 \end{bmatrix}$. Dessa två vektorer utgör en grund för vektorutrymmet som beskriver kvantbitens tillstånd. Det innebär att alla kvanttillståndsvektorer kan skrivas som en summa av dessa basvektorer. Mer specifikt kan vektorn $\begin{bmatrix} x \\ y \end{bmatrix}$ skrivas som $x \begin{bmatrix} 1 \\ 0 \end{bmatrix} + y \begin{bmatrix} 0 \\ 1 \end{bmatrix}$. Även om varje rotation av dessa vektorer skulle fungera som en helt giltig grund för kvantbiten, väljs den här specifika genom att kalla den beräkningsbasen.

Dessa två kvanttillstånd tas för att motsvara de två tillstånden för en klassisk bit, nämligen $0$ och $1$. Standardkonventionen är att välja

$$0\equiv\begin{bmatrix} 1 \\ 0 \end{bmatrix}$$$$1 \equiv\begin{bmatrix} 0 \\ 1 \end{bmatrix},$$

även om det motsatta valet lika gärna skulle kunna tas. Av det oändliga antalet möjliga kvanttillståndsvektorer med en kvantbit motsvarar endast två tillstånd av klassiska bitar. alla andra kvanttillstånd gör det inte.

Mäta en kvantbit

Genom att förklara hur man representerar en qubit kan man få viss intuition för vad dessa tillstånd representerar genom att diskutera begreppet mätning. En mätning motsvarar den informella idén att "titta" på en kvantbit, som omedelbart kollapsar kvanttillståndet till ett av de två klassiska tillstånden $\begin{bmatrix} 1 \\ 0 \end{bmatrix}$ eller $\begin{bmatrix} 0 \\ 1 \end{bmatrix}$. När en kvantbit som anges av kvanttillståndsvektorn $\begin{bmatrix}\alpha\\\beta\end{bmatrix}$mäts erhålls utfall $0$ med sannolikhet $|\alpha|^2$ och utfall $1$ med sannolikhet $|\beta|^2.$ På utfall $0$ är $\begin{bmatrix} kvantbitens nya tillstånd 1 \\ 0 \end{bmatrix}$; på utfall $1$ är $\begin{bmatrix} dess tillstånd 0 \\ 1 \end{bmatrix}$. Observera att dessa sannolikheter summerar upp till $1$ på grund av normaliseringsvillkoret $|\alpha|^2 + |\beta|^2 = 1$.

Mätningens egenskaper innebär också att det övergripande tecknet för kvanttillståndsvektorn är irrelevant. Att negera en vektor motsvarar $\alpha\rightpilen -\alpha$ och $\beta\rightpilen -\beta$. Eftersom sannolikheten för att mäta $0$ och $1$ beror på termernas storlek i kvadrat ändrar infogning av sådana tecken inte sannolikheten alls. Sådana faser kallas &ofta quot;globala faser" och mer allmänt kan vara av formatet $e^{i \phi}$ snarare än bara $\pm 1$.

En sista viktig egenskap för mätning är att den inte nödvändigtvis skadar alla kvanttillståndsvektorer. Om man börjar med en qubit i tillståndet $\begin{bmatrix} 1 \\ 0 \end{bmatrix}$, vilket motsvarar det klassiska tillståndet $0$, ger mätning av det här tillståndet alltid resultatet $0$ och lämnar kvanttillståndet oförändrat. Om det bara finns klassiska bitar (till exempel kvantbitar som antingen är $\begin{bmatrix}1 \\ 0 \end{bmatrix}$ eller $\begin{bmatrix}0 \\ 1 \end{bmatrix}$) skadar mätningen inte systemet. Det innebär att man kan replikera klassiska data och manipulera dem på en kvantdator precis som man kan göra på en klassisk dator. Möjligheten att lagra information i båda tillstånden samtidigt är dock det som höjer kvantberäkning utöver vad som är möjligt klassiskt och ytterligare berövar kvantdatorer möjligheten att kopiera kvantdata urskillningslöst, se även no-cloning-sats.

Visualisera kvantbitar och transformeringar med bloch-sfären

Qubits kan också avbildas i $3D$ med Blochs sfärrepresentation. Bloch-sfären ger ett sätt att beskriva ett kvanttillstånd med en kvantbit (som är en tvådimensionell komplex vektor) som en tredimensionell verklig värdevektor. Detta är viktigt eftersom det gör att vi kan visualisera enstaka qubit-tillstånd och därmed utveckla resonemang som kan vara ovärderliga för att förstå multi-qubit-tillstånd (där bloch-sfärrepresentationen tyvärr bryts ned). Bloch-sfären kan visualiseras på följande sätt:

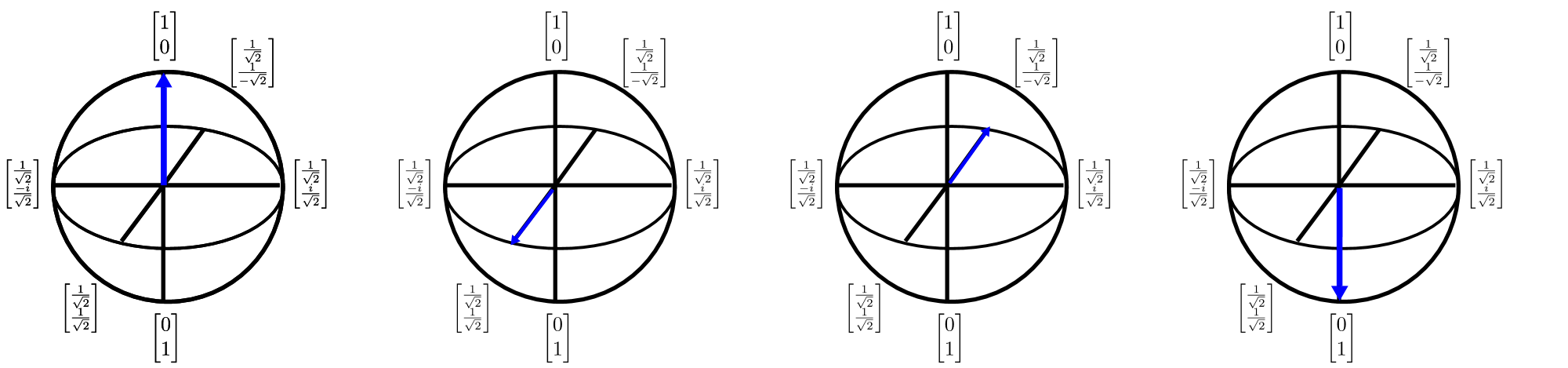
Bloch-sfär

Pilarna i det här diagrammet visar i vilken riktning kvanttillståndsvektorn pekar och varje omvandling av pilen kan betraktas som en rotation om en av kardinalaxlarna. Även om det är en kraftfull intuition att tänka på en kvantberäkning som en sekvens av rotationer, är det svårt att använda denna intuition för att utforma och beskriva algoritmer. Q# lindrar problemet genom att tillhandahålla ett språk för att beskriva sådana rotationer.

Operationer med en kvantbit

Kvantdatorer bearbetar data genom att använda en universell uppsättning kvantgrindar som kan emulera valfri rotation av kvanttillståndsvektorn. Begreppet universalitet liknar begreppet universalitet för traditionell (till exempel klassisk) databehandling där en grinduppsättning anses vara universell om varje transformering av indatabitarna kan utföras med hjälp av en krets av begränsad längd. Inom kvantberäkning är de giltiga transformeringar som vi får utföra på en kvantbit enhetstransformeringar och mätningar. Den angränsande åtgärden eller den komplexa konjugattransponeringen är av avgörande betydelse för kvantberäkning eftersom den behövs för att invertera kvanttransformeringar.

Enkelt kvantbitsoperationer, eller även kallade enkvantskvantgrindar, kan klassificeras i två kategorier: Clifford-grindar och icke-Clifford-grindar. Icke-Clifford-grindar består endast av $T-gate$ (även kallat $\pi/8-grinden$ ).

$$ T=\begin{bmatrix} 1 & 0 \ 0 & e^{i\pi/4}\end{bmatrix}. $$

Standarduppsättningen med Clifford-portar med enkel qubit, som ingår som standard i Q#, inkluderar

$$ H=\frac{{1}{\sqrt{{2}}\begin{bmatrix} 1 & 1 \ 1 &-1 \end{bmatrix} , \qquad S =\begin{bmatrix} 1 & 0 \ 0 & i \end{bmatrix}= T^2, \qquad X=\begin{bmatrix} 0 & 1 \ 1& 0 \end{bmatrix}= HT^4H, $$

$$ Y =\begin{bmatrix} 0 & -i \ i & 0 \end{bmatrix}=T^2HT^4 HT^6, \qquad Z=\begin{bmatrix}1&0\ 0&-1 \end{bmatrix}=T^4. $$

Här används åtgärderna $X$, $Y$ och $Z$ särskilt ofta och får namnet Pauli-operatorer efter deras skapare Wolfgang Pauli. Tillsammans med icke-Clifford-porten $(T-porten$) kan dessa operationer komponeras för att approximera valfri enhetär transformation på en enskild kvantbit.

Medan föregående utgör de mest populära primitiva portarna för att beskriva åtgärder på den logiska nivån i stacken (tänk på den logiska nivån som nivån för kvantalgoritmen), är det ofta praktiskt att överväga mindre grundläggande åtgärder på algoritmisk nivå, till exempel åtgärder närmare en funktionsbeskrivningsnivå. Lyckligtvis har Q# också metoder som är tillgängliga för implementering av unitära operationer på högre nivå, vilket i sin tur möjliggör att algoritmer på hög nivå kan implementeras utan att uttryckligen dela upp allt till Clifford- och $T$-gates.

Den enklaste sådan primitiv är en enkel qubit-rotation. Tre rotationer med en kvantbit beaktas vanligtvis: $R_x$, $R_y$ och $R_z$. Om du till exempel vill visualisera rotationsåtgärden $R_x(\theta)$ kan du tänka dig att du pekar höger tumme längs riktningen $för blockh-sfärens x-axel$ och roterar vektorn med handen genom en vinkel av $\theta/2$ radianer. Den här förvirrande faktorn $2$ beror på att ortogonala vektorer är $180^\circ$ när de ritas på Bloch-sfären, men faktiskt $är 90^\circ$ ifrån varandra geometriskt. Motsvarande enhetsmatriser är:

$$ \begin{align*}& R_z(\theta) = e^{-i\theta Z/2}=\begin{bmatrix} e^{-i\theta/2}& 0\\ 0& e^{i\theta/2}\end{bmatrix}, \\& R_x(\theta) = e^{-i\theta X/2}= HR_z(\theta)H =\begin{bmatrix} \cos(\theta/2) & -i\sin(\theta/2)\\ -i\sin(\theta/2) & \cos(\theta/2) \end{bmatrix}, \\& R_y(\theta) = e^{-i\theta Y/2}= SHR_z(\theta)HS^\dagger=\begin{bmatrix} \cos(\theta/2) & -\sin(\theta/2)\\ \sin(\theta/2) & \cos(\theta/2) \end{bmatrix}. \end{justera*}$$

Precis som alla tre rotationer kan kombineras för att utföra en godtycklig rotation i tre dimensioner, kan det ses från Bloch-sfärrepresentationen att alla enhetsmatriser också kan skrivas som en sekvens med tre rotationer. Mer specifikt för varje enhetsmatris $U$ finns $\alpha,\beta,\gamma,\delta$ så att $U= e^{i\alpha} R_x(\beta)R_z(\gamma)R_x(\delta)$. Därför bildar $R_z(\theta)$ och $H$ också en universell uppsättning av grindar, även om det inte är en diskret uppsättning eftersom $\theta$ kan ta valfritt värde. Därför, och på grund av tillämpningar inom kvantsimulering, är sådana kontinuerliga grindar avgörande för kvantberäkning, särskilt på nivå av kvantalgoritmdesign. För att uppnå feltolerant maskinvaruimplementering kommer de slutligen att kompileras till diskreta grindsekvenser som nära approximerar dessa rotationer.

Relaterat innehåll