幾何著色器 (GS) 階段
幾何著色器 (GS) 階段會負責處理整個原始物件:三角形、線條、點及其相鄰頂點。 它適用於許多演算法,包括點原件展開、動態粒子系統,以及陰影磁碟區產生。 它可支援幾何放大和取消放大。
幾何著色器階段會處理整個原始物件:三角形 (3 個頂點,且最多會有 3 個相鄰頂點)、線條 (2 個頂點,且最多會有 2 個相鄰頂點) 和點 (1 個頂點)。
幾何著色器也支援有限的幾何放大和取消放大。 只要提供一個原始物件,幾何著色器就能捨棄原始物件,或發出一個或多個新的原始物件。
幾何著色器 (GS) 階段為可進行程式設計的著色器階段;會透過圖形管線圖表中的圓角區塊加以表示。 這個著色器階段會公開自身專屬的獨特功能,該功能是以著色器模型為基礎所建置而成 (請參閱通用著色器核心)。
幾何著色器階段相當適合運用在演算法上,包括:
- 點原件展開
- 動態粒子系統
- 毛皮/魚鰭產生
- 陰影磁碟區產生
- 單通道轉譯至立方體貼圖
- 每一原始物件材質交換
- 每一原始物件材質設定 - 這項功能會包括產生重心座標,以做為原始物件資料,好讓像素著色器能執行自訂的屬性插補。
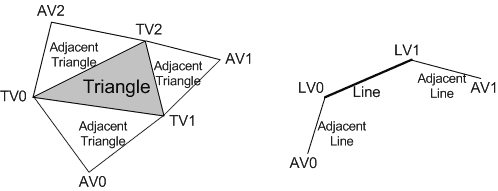
幾何著色器階段會執行應用程式特定的著色器程式碼,並使用整個原始物件做為輸入,另外也可在輸出中產生頂點。 不同於在單一頂點上運作的頂點著色器,幾何著色器的輸入為完整原始物件的頂點 (三角形為三個頂點、線條為兩個頂點,而點則為單一頂點)。 幾何著色器也能帶入邊緣相鄰原始物件的頂點資料,以做為輸入 (三角形為另外三個頂點,線條則為另外兩個頂點)。
幾何著色器階段可使用輸入組合語言 (IA) 階段自動產生的 SV_PrimitiveID 系統產生值。 如此就能在想要的時候擷取或計算每一原始物件資料。
幾何著色器為作用中時,就會叫用稍早在管線中傳遞或產生的每個原始物件。 每一次的幾何著色器叫用作業,都會視為為輸入叫用原始物件的資料,無論該資料為單一點、單一線條或單一三角形。 來自先前管線的三角形寬帶,會導致叫用寬帶中每個個別三角形的幾何著色器 (如同寬帶已展開至三角形清單中)。 個別原始物件中每個頂點的所有輸入資料都可供使用 (也就是三角形的 3 個頂點),如果適用且有提供,還會包含相鄰頂點資料。
常見的頂點縮寫:
| 縮寫 | 術語 |
|---|---|
| TV | 三角形頂點 |
| LV | 線條頂點 |
| AV | 相鄰頂點 |
幾何著色器 (GS) 階段可輸出多個頂點,以形成單一選取拓撲。 可用的幾何著色器拓撲會包括 tristrip、linestrip 和 pointlist。 任何幾何著色器叫用中發出的原始物件數量可自由變化,不過,可發出之頂點數量上限,則必須透過靜態方式加以宣告。 幾何著色器叫用所發出的寬帶長度可以是任意長度,而新的寬帶則能透過 RestartStrip HLSL 函式建立。
除了新增至串流的資料則為序列之外,執行幾何著色器執行個體的作業需搭配其他叫用來完成。 幾何著色器的指定叫用輸出獨立於其他叫用之外 (雖然會依循順序)。 產生三角寬帶的幾何著色器將於每次叫用時啟動新的寬帶。
幾何著色器輸出可透過資料流輸出階段饋送至轉譯器階段和/或記憶體中的頂點緩衝區。 饋送至記憶體的輸出會展開至個別點/線條/三角形清單 (和傳遞至轉譯器的情況完全相同)。
幾何著色器會透過將頂點附加至輸出串流物件的方式,每次針對一個頂點輸出資料。 串流拓撲會透過固定宣告來判斷,以選擇 TriangleStream、LineStream 和 PointStream 做為 GS 階段的輸出。
可用的串流物件類型共有三種:TriangleStream、LineStream 和 PointStream,三者皆為範本化物件。 輸出拓撲會依照各自的物件類型來判斷,而附加至串流的頂點格式則會透過範本類型來判斷。
當幾何著色器輸出已識別為系統解譯值 (例如 SV_RenderTargetArrayIndex 或 SV_Position) 時,除了可將資料本身傳遞至下一個著色器階段,以做為輸出之用外,硬體還會查看這項資料,並執行與值相依的部分行為。 如果來自幾何著色器的此類型資料輸出對硬體而言具有每一原始物件基礎 (例如 SV_RenderTargetArrayIndex 或 SV_ViewportArrayIndex) 的意義,而非每一頂點基礎 (例如 SV_ClipDistance[n] 或 SV_Position) 的意義,就會帶入原始物件發出之前置頂點所提供的每一原始物件資料。
如果幾何著色器結束,且原始物件不完整,則可透過幾何著色器產生部分完成的原始物件。 不完整的原始物件會透過無訊息的方式捨棄。 這和 IA 用來處理部分完成之原始物件的方式相似。
幾何著色器可於不需要螢幕空間導數處,執行載入和紋理取樣作業 (samplelevel、samplecmplevelzero、samplegrad)。