Kuantum bilişiminde kubit
Bitler klasik bilgi işlemdeki bilgilerin temel nesnesi olduğu gibi kubitler de (kuantum bitleri) kuantum bilişimindeki bilgilerin temel nesnesidir. Bu yazışmayı anlamak için bu makalede en basit örneğe bakabilirsiniz: tek bir kubit.
Kubiti temsil etme
Bit veya ikili basamak 0 veya $1 değerine sahip olsa da $$kubitin değeri 0$, $1$ veya kuantum süper pozisyonu $0$$ ve $1$$ olabilir.
Tek bir kubitin durumu, birim normunun iki boyutlu sütun vektörünün ( yani girdilerinin büyüklüğünün karesinin 1$ olarak toplamı $gerekir) açıklanabilir. Kuantum durumu vektörsü olarak adlandırılan bu vektör, tek kubitli kuantum sistemini tanımlamak için gereken tüm bilgileri, aynı tek bitin ikili değişkenin durumunu tanımlamak için gereken tüm bilgileri barındırdığı gibi tutar. Kuantum bilişimindeki vektörlerin ve matrislerin temelleri için bkz . Vektör ve matrisler.
Norm $1$ ile gerçek veya karmaşık sayıların iki boyutlu sütun vektörleri, kubit tarafından tutulan olası bir kuantum durumunu temsil eder. Dolayısıyla $\begin{bmatrix}\\\beta\alpha\end{bmatrix}$ ve karmaşık sayılar ^2 + |\beta|^=2 1'i $|\alpha|$karşılayan bir kubit durumunu $\alpha$ $\beta$ temsil eder. Kubitleri temsil eden geçerli kuantum durumu vektörlerine bazı örnekler şunlardır:
$$\begin{bmatrix}1 \\ 0 \end{bmatrix}, \begin{bmatrix} 0 \\ 1 \end{bmatrix},\frac{\\\end{bmatrix}{1}{\sqrt{2}}\begin{bmatrix}\frac{{1}{\sqrt{2}} ,\frac{1}{\sqrt{\begin{bmatrix}{2}}\end{bmatrix}\\\text{\frac{{-1}{\sqrt{2}} ve\\\frac{\frac{1}{\sqrt{{2}}}\begin{bmatrix} i.}{\sqrt{2}}\end{bmatrix}$$
Kuantum durumu vektörleri $\begin{bmatrix} 1 \\ 0 \end{bmatrix}$ ve $\begin{bmatrix} 0 \\ 1 \end{bmatrix}$ özel bir rol alır. Bu iki vektör, kubitin durumunu açıklayan vektör alanı için bir temel oluşturur. Bu, herhangi bir kuantum durumu vektörünün bu temel vektörlerin toplamı olarak yazılabilmesi anlamına gelir. Özellikle, x \\ y vektöru $\begin{bmatrix} x \begin{bmatrix} 1 \\ 0 + y \begin{bmatrix} 0 \end{bmatrix} \\ 1 \end{bmatrix}$olarak $yazılabilir\end{bmatrix}$. Bu vektörlerin herhangi bir döndürmesi kubit için mükemmel geçerli bir temel görevi görecek olsa da, hesaplama temeli olarak adlandırılarak bu özel bir temel seçilir.
Bu iki kuantum durumu, klasik bitin $iki durumu olan 0$ ve $1'e$ karşılık gelir. Standart kural,
$$0\equiv\begin{bmatrix} 1 \\ 0 \end{bmatrix}, \qquad 1 \equiv\begin{bmatrix} 0 \\ 1 \end{bmatrix},$$
ancak karşıt seçim de aynı derecede iyi bir şekilde alınabilir. Bu nedenle, olası tek kubit kuantum durumu vektörlerinin sonsuz sayıdan yalnızca ikisi klasik bit durumlarına karşılık gelir; diğer tüm kuantum durumları bunu yapmaz.
Kubit ölçme
Bir kubitin nasıl temsil edildiğinin açıklanması, ölçüm kavramını tartışarak bu durumların neyi temsil ettiği konusunda bazı sezgiler elde edebilir. Ölçüm, kuantum durumunu hemen iki klasik durumdan $\begin{bmatrix} birine daraltan 1 0 veya \\ $\begin{bmatrix} \end{bmatrix}$0 \end{bmatrix}$ 1 \\ olan bir kubite "bakma" fikrine karşılık gelir. Kuantum durumu vektör $\begin{bmatrix}\end{bmatrix}$\\\beta\alphatarafından verilen bir kubit ölçüldüyse, 0$ sonucu $^2$ olasılığıyla$|\alpha|, sonuç $1$ ise ^2$ olasılığıyla $|\beta|elde edilir. Sonuç $0'da$ kubitin yeni durumu 1 \\ 0 \end{bmatrix}$olur$\begin{bmatrix}; sonuç $1'de$ durumu 0 \\ 1 \end{bmatrix}$olur$\begin{bmatrix}. ^2 + ^2 1 normalleştirme koşulu $|\alpha|nedeniyle bu olasılıkların 1'e $$$ kadar toplandığını unutmayın.= |\beta|
Ölçümün özellikleri, kuantum durum vektörünün genel işaretinin ilgisiz olduğu anlamına da gelir. Vektöre olumsuzluk eklemek ok ve\right$\beta\alpha$ ok ile $\alpha\right\beta$eşdeğerdir. 0$ ve $1'i$ ölçme $olasılığı terimlerin büyüklüğüne bağlı olduğundan, bu tür işaretlerin eklenmesi olasılıkları değiştirmez. Bu tür aşamalar genellikle quot olarak adlandırılır&;genel aşamalar" ve daha genel olarak yalnızca $\pm 1$ yerine e^{i \phi}$ biçiminde $olabilir.
Ölçümün son önemli özelliği, tüm kuantum durumu vektörlerine zarar vermemesidir. Biri klasik durum 0'a$$ karşılık gelen 10 \end{bmatrix}$\\ durumundaki $\begin{bmatrix} bir kubitle başlarsa, bu durumu ölçmek her zaman 0$ sonucunu $verir ve kuantum durumunu değiştirmeden bırakır. Bu anlamda, yalnızca klasik bitler varsa (örneğin, 1 0 veya $\begin{bmatrix}0 \end{bmatrix}$ \\ 1 \\ \end{bmatrix}$olan $\begin{bmatrix}kubitler) ölçüm sisteme zarar vermez. Bu, klasik verileri çoğaltabileceği ve bir kuantum bilgisayarda aynı klasik bilgisayarda olduğu gibi işleyebileceği anlamına gelir. Bununla birlikte, bilgileri her iki durumda da aynı anda depolama yeteneği, kuantum bilişimini klasik olarak mümkün olanın ötesine yükselten ve kuantum verilerini ayrım gözetmeden kopyalama yeteneğine sahip kuantum bilgisayarları daha da soyan özelliktir. Ayrıca kopyalama yok teoremine de bakın.
Bloch küresini kullanarak kubitleri ve dönüşümleri görselleştirme
Kubitler Bloch sphere gösterimi kullanılarak 3B$olarak $da resmedilebilir. Bloch küresi, tek kubitli kuantum durumunu (iki boyutlu karmaşık bir vektördür) üç boyutlu gerçek değerli bir vektör olarak tanımlamanın bir yolunu sunar. Bu önemlidir çünkü tek kubitli durumları görselleştirmemize ve böylece çok kubitli durumları anlamada değerli olabilecek bir mantık geliştirmemize olanak tanır (ne yazık ki Bloch küre gösterimi bozulur). Bloch küresi aşağıdaki gibi görselleştirilebilir:
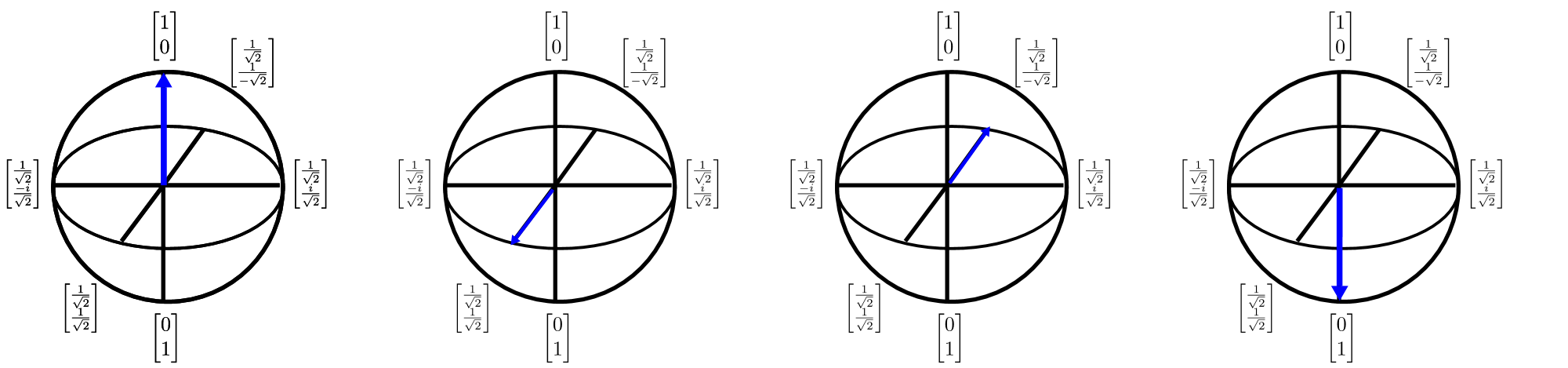
Bu diyagramdaki oklar, kuantum durum vektörünün işaret ettiği yönü gösterir ve okun her dönüşümü, kardinal eksenlerden biri hakkında bir döndürme olarak düşünülebilir. Bir kuantum hesaplamasını döndürme dizisi olarak düşünmek güçlü bir sezgi olsa da, algoritmaları tasarlamak ve açıklamak için bu sezgiyi kullanmak zordur. Q# bu tür döndürmeleri açıklamaya yönelik bir dil sağlayarak bu sorunu giderir.
Tek kubitli işlemler
Kuantum bilgisayarlar, kuantum durumu vektörünün herhangi bir döndürmesine öykünebilen evrensel bir kuantum kapısı kümesi uygulayarak verileri işler. Bu evrensellik, giriş bitlerinin her dönüşümü sonlu bir uzunluk devresi kullanılarak gerçekleştirilebiliyorsa, bir kapı kümesinin evrensel olarak kabul edildiği geleneksel (örneğin klasik) bilgi işlem için evrensellik olgusunun bir benzerliğidir. Kuantum bilişiminde, kubit üzerinde gerçekleştirmemize izin verilen geçerli dönüşümler, birimsel dönüşümler ve ölçümdür. Kuantum dönüşümlerini ters çevirmek için gerektiğinden, bitişik işlem veya karmaşık eşlem transpozülleri kuantum bilişimi için çok önemlidir.
Tek kubitli işlemler veya tek kubitli kuantum geçitleri iki kategoride sınıflandırılabilir: Clifford geçitleri ve Clifford olmayan kapılar. Clifford olmayan kapılar yalnızca T$ kapısı ($\pi/8$ kapısı olarak $da bilinir) oluşur.
$$T=\begin{bmatrix} 1 amp; 0 \\ 0 & e^{i\pi/4}\end{bmatrix}.& $$
içinde varsayılan olarak Q#dahil edilen tek kubitli Clifford geçitlerinin standart kümesi dahil
$$H=\frac{{1}{\sqrt{{2}}\begin{bmatrix} 1 & 1 1 &\\ amp;-1 \end{bmatrix} , \qquad S =\begin{bmatrix} 1 & 0 \\ 0 & i \end{bmatrix}= T^2, \qquad X=\begin{bmatrix} 0 & 1 \\ 1& 0 \end{bmatrix}= HT^4H,$$
$$ Y =\begin{bmatrix} 0 & -i \\ i & 0 \end{bmatrix}=T^2HT^4 HT^6, \qquad Z=\begin{bmatrix}1& 0\\ 0&&-1 \end{bmatrix}=T^4. $$
Burada X$, $Y$ ve $Z$ işlemleri $özellikle sık kullanılır ve oluşturucuları Wolfgang Pauli'den sonra Pauli operatörleri olarak adlandırılır. Clifford olmayan kapı ( $T$ kapısı) ile birlikte, bu işlemler tek bir kubit üzerindeki tüm birimsel dönüşümleri yaklaşık olarak oluşturmak için oluşturulabilir.
Önceki, yığının mantıksal düzeyindeki işlemleri tanımlamak için en popüler ilkel geçitleri oluştursa da (mantıksal düzeyi kuantum algoritmasının düzeyi olarak düşünün), genellikle algoritma düzeyinde daha az temel işlemleri(örneğin işlev açıklaması düzeyine yakın işlemler) göz önünde bulundurmak uygundur. Neyse ki, Q# clifford ve $T-gates'e$ kadar her şeyi açıkça ayrıştırmadan üst düzey algoritmaların uygulanmasına olanak tanıyan daha üst düzey üniteler uygulamak için de yöntemler mevcuttur.
Bu tür en basit ilkel, tek kubit döndürmedir. Genellikle üç tek kubit döndürmesi dikkate alınır: $R_x$, $R_y$ ve $R_z$. Örneğin, döndürme $R_x(\teta)$ eylemini görselleştirmek için sağ başparmağını Bloch küresinin $x$ ekseni yönünde işaret edip elinle vektörün \teta/2$ radyan açıyla $döndürülmesini düşünün. 2'nin $$ bu kafa karıştırıcı faktörü, ortogonal vektörlerin $Bloch küresi üzerinde çizildiğinde birbirinden 180^\circ$ olması gerçeğinden kaynaklanır, ancak geometrik $olarak birbirinden 90^\circ$ derece ayrılır. Karşılık gelen ünite matrisleri şunlardır:
\begin{align*}& R_z(\teta) = e^{-i\theta Z/2}=\begin{bmatrix} e^{-i\teta/2}& 0\\ 0& e^{i\teta/2\end{bmatrix}}, \\& R_x(\teta) e^{-i\theta X/2=} HR_z(\theta)H =\begin{bmatrix} \cos(\theta/2) & -i\sin(\theta/2)\\ -i\sin(\theta/2) & \cos(\theta/2) \end{bmatrix}, \\& = R_y(\theta) e^-i\theta Y/2=} SHR_z(\theta)HS^\begin{bmatrix}\dagger= \cos(\theta/2) & -\sin(\theta/2)\\ \sin(\teta/2) & \cos(\theta/2) \end{bmatrix}.{= \end{hizalamak*}
Üç boyutta rastgele bir döndürme gerçekleştirmek için herhangi bir üç döndürme birlikte birleştirilebildiği gibi, Bloch küre gösteriminden herhangi bir ünite matrisinin de üç döndürme dizisi olarak yazılabildiği görülebilir. Özellikle, U olan her birim matris $$ için U\gamma\beta\delta$ e^{i\alpha} R_x()R_z(\beta)R_x(\gamma\delta)gibi$$= , vardır$\alpha. Bu nedenle $R_z(\theta)$ ve $H$ de evrensel bir kapı kümesi oluşturur, ancak \theta$ herhangi bir değer alabildiği için $ayrık bir küme değildir. Bu nedenle ve kuantum simülasyonundaki uygulamalardan dolayı, bu tür sürekli geçitler özellikle kuantum algoritması tasarım düzeyinde kuantum hesaplaması için çok önemlidir. Hataya dayanıklı donanım uygulaması elde etmek için, bunlar sonunda bu döndürmelere yakın olan ayrık kapı dizilerinde derlenir.