A qubit a kvantum-számítástechnikában

  • Cikk

Ahogyan a bitek a klasszikus számítástechnika alapvető információobjektumai, a qubitek (kvantumbitek) a kvantum-számítástechnika alapvető információobjektumai. A levelezés megértéséhez ez a cikk a legegyszerűbb példát vizsgálja: egyetlen qubitet.

Qubit ábrázolása

Míg egy bit vagy bináris számjegy értéke lehet 0 vagy 1, a qubitek értéke $lehet 0$, $1$ vagy 0$ és $1$ kvantum szuperpozíció$.$$$$

Egy qubit állapotát az egységnormák kétdimenziós oszlopvektorával lehet leírni, azaz a bejegyzések négyzetének négyzetét 1-re$ kell összeadni$. Ez a kvantumállapotvektornak nevezett vektor az egy qubites kvantumrendszer leírásához szükséges összes információt tartalmazza, ahogyan egyetlen bit tartalmazza a bináris változó állapotának leírásához szükséges összes információt. A vektorok és mátrixok kvantum-számítástechnikában való alapjaiért lásd: Lineáris algebra a kvantum-számítástechnikához , vektorok és mátrixok.

Az 1$. normával $rendelkező valós vagy komplex számok bármely kétdimenziós oszlopvektora egy qubit által tartott lehetséges kvantumállapotot jelöl. Így $\begin{bmatrix}\alpha\\\beta\end{bmatrix}$ egy qubit-állapotot jelöl, ha $\alpha$ és $\beta$ komplex számok, amelyek megfelelnek a(z) $|\alpha|^2 + |\beta|^2 = 1$ értéknek. Néhány példa a qubiteket képviselő érvényes kvantumállapot-vektorokra:

$$\begin{bmatrix}1 \\ 0 \end{bmatrix}, \begin{bmatrix} 0 \\ 1 \end{bmatrix},\frac{\frac{\begin{bmatrix}{1}{\sqrt{2}}\\\end{bmatrix}{1}{\sqrt{2}} ,\frac{1}{\sqrt{\end{bmatrix}\begin{bmatrix}\frac{\\{-1}{\sqrt{2}}{2}} és\\{2}}\frac{}\begin{bmatrix}\frac{1}{\sqrt{\text{ i.}{\sqrt{2}}\end{bmatrix}$$

Az 1 0 és $\begin{bmatrix} 0 \end{bmatrix}$\\ 1 \\\end{bmatrix}$ kvantumállapot-vektorok $\begin{bmatrix} különleges szerepet töltenek be. Ez a két vektor képezi a qubit állapotát leíró vektortér alapját. Ez azt jelenti, hogy bármely kvantumállapot-vektor megírható ezen alapvektorok összegeként. Pontosabban az x y vektor $\begin{bmatrix} x \begin{bmatrix} 1 \\ 0 \end{bmatrix} + y \begin{bmatrix} 0 \\ 1 \end{bmatrix}$formátumban írható$.\end{bmatrix}$\\ Bár a vektorok bármilyen forgása tökéletesen érvényes alapként szolgálna a qubithez, ezt a konkrétat választja ki a számítási alapnak nevezve.

Ez a két kvantumállapot egy klasszikus bit két állapotának felel meg, nevezetesen $a 0-nak$ és $az 1-nek$. A szabványos konvenció az, hogy

$$0\equiv\begin{bmatrix} 1 \\ 0 \end{bmatrix}, \qquad 1 \equiv\begin{bmatrix} 0 \\ 1 \end{bmatrix},$$

bár az ellenkező választás is jól meghozható. Így a lehetséges egy qubites kvantumállapot-vektorok végtelen számából csak kettő felel meg a klasszikus bitek állapotainak; minden más kvantumállapot nem.

Qubit mérése

A magyarázott qubitek ábrázolásának módjával némi intuíciót kaphatunk arról, hogy ezek az állapotok mit jelentenek a mérés fogalmának megvitatásával. A mérés megfelel a qubitek "nézésének" informális elképzelésének, amely azonnal összecsukja a kvantumállapotot a két klasszikus állapot $\begin{bmatrix} egyikével 1 \\ 0 \end{bmatrix}$ vagy $\begin{bmatrix} 0 \\ 1 \end{bmatrix}$. A kvantumállapot-vektor $\begin{bmatrix}\alpha\\\end{bmatrix}$\betaáltal megadott qubit mérésekor a 0$ eredményt $^2 valószínűséggel$|\alpha|, az 1$. eredményt $pedig ^2$$ valószínűséggel $|\beta|kapja meg. A 0. eredmény $esetében a qubit új állapota $\begin{bmatrix} 1 \\ 0\end{bmatrix}$; az 1$. eredmény $esetében az $\begin{bmatrix} állapota 0 \\ 1 \end{bmatrix}$.$ Vegye figyelembe, hogy ezek a valószínűségek a(z) ^2 + |\beta|^2 = 1$ normalizációs feltétel $|\alpha|miatt legfeljebb $1-et összegeznek$.

A mérés tulajdonságai azt is jelentik, hogy a kvantumállapot-vektor általános jele irreleváns. A vektorok tagadása egyenértékű a $\alpha\rightnyíllal és\alpha$$\beta\righta nyíllal\beta$. Mivel a 0$ és $az 1$ mérésének $valószínűsége a kifejezések négyzetének nagyságától függ, az ilyen jelek beszúrása nem változtatja meg a valószínűségeket. Ezeket a fázisokat gyakran idézőjelnek nevezik&;global phases" és általában lehet e^{i \phi}$ formátumú$, nem csak $\pm 1$.

A mérés végső fontos tulajdonsága, hogy nem feltétlenül károsítja az összes kvantumállapot-vektort. Ha az egyik 1 0 állapotú $\begin{bmatrix} qubittel kezdődik, amely a klasszikus 0$\end{bmatrix}$ állapotnak $felel meg, az állapot mérése mindig a 0$ eredményt $adja, és változatlanul hagyja a kvantumállapotot.\\ Ebben az értelemben, ha csak klasszikus bitek vannak (például 1 0 vagy $\begin{bmatrix}0 \end{bmatrix}$\\ 1 \\\end{bmatrix}$qubitek$\begin{bmatrix}), akkor a mérés nem károsítja a rendszert. Ez azt jelenti, hogy a klasszikus adatokat ugyanúgy lehet replikálni és kezelni egy kvantumszámítógépen, mint egy klasszikus számítógépen. Az a képesség azonban, hogy az információkat mindkét állapotban egyszerre tárolja, az emeli a kvantum-számítástechnikát azon túl, ami klasszikusan lehetséges, és tovább megfosztja a kvantumszámítógépeket a kvantumadatok válogatás nélküli másolásának képességétől, lásd még a klónozás nélküli tételt is.

Qubitek és átalakítások vizualizációja a blochgömb használatával

A qubitek 3$D-ben $is ábrázolhatók a Bloch-gömb ábrázolása segítségével. A Bloch-gömb egy egy qubites kvantumállapot (amely egy kétdimenziós komplex vektor) háromdimenziós, valós értékű vektorként való leírására szolgál. Ez azért fontos, mert lehetővé teszi az egy qubites állapotok vizualizációját, és ezáltal olyan érvelés kialakítását, amely felbecsülhetetlen értékű lehet a több qubites állapotok megértésében (ahol sajnos a Bloch-gömb ábrázolása lebomlik). A Bloch-gömb a következőképpen jeleníthető meg:

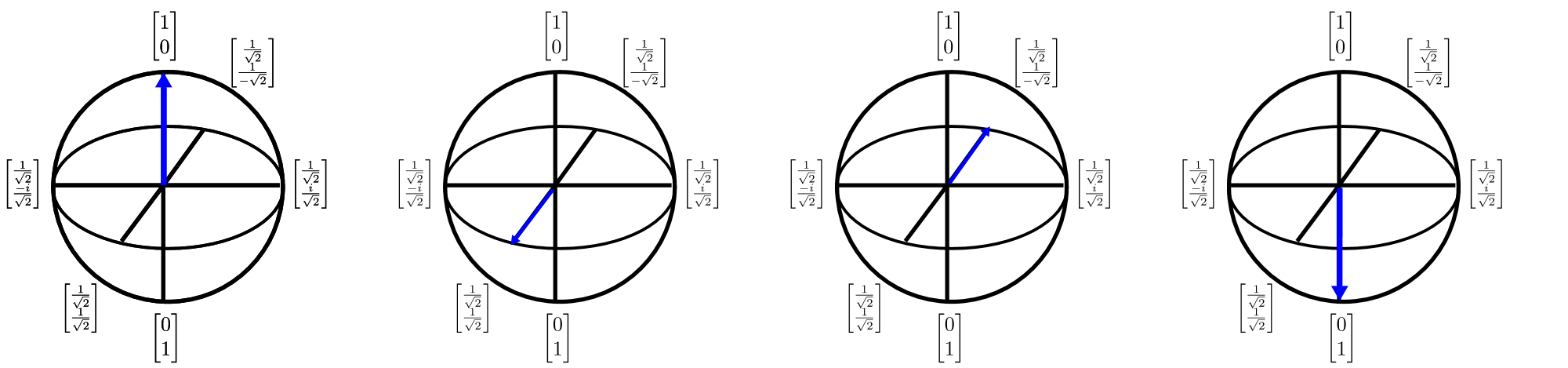
Bloch-gömb

A diagram nyilai azt az irányt mutatják, amelyben a kvantumállapot-vektor mutat, és a nyíl minden egyes transzformációja úgy tekinthető, mint az egyik kardinális tengely elforgatása. Bár a kvantumszámítások rotációk sorozataként való gondolkodása hatékony megérzés, az algoritmusok tervezéséhez és leírásához nehéz ezt az intuíciót használni. Q# az ilyen rotációk leírására szolgáló nyelv biztosításával enyhíti ezt a problémát.

Egy qubites műveletek

A kvantumszámítógépek olyan univerzális kvantumkapuk alkalmazásával dolgozzák fel az adatokat, amelyek képesek a kvantumállapot-vektor bármilyen forgását emulálni. Az egyetemesség ezen fogalma hasonló a hagyományos (például klasszikus) számítástechnika univerzális fogalmához, ahol a kapukészletet univerzálisnak tekintik, ha a bemeneti bitek minden átalakítása véges hosszúságú kapcsolatcsoporttal végezhető el. A kvantum-számítástechnikában a qubiten végrehajtható érvényes átalakítások egységes átalakítások és mérések. A szomszédos művelet vagy az összetett konjugált transzponálás rendkívül fontos a kvantum-számítástechnika szempontjából, mivel a kvantumátalakítások invertálásához szükséges.

Az egy qubites műveletek vagy az egy qubites kvantumkapuk két kategóriába sorolhatók: Clifford-kapuk és nem Clifford-kapuk. A nem Clifford kapuk csak $t-kapuból$ (más néven $\pi/8$ kapuból) állnak.

$$T=\begin{bmatrix} 1 amp; 0 \\ 0 & e^{i\pi/4}\end{bmatrix}.& $$

Az egy qubites Clifford-kapuk standard készlete, alapértelmezés szerint tartalmazza a Q#következőket:

$$H=\frac{{1}{\sqrt{{2}}\begin{bmatrix} 1 & 1 \\ 1 &-1 \end{bmatrix} , \qquad S =\begin{bmatrix} 1 & 0 0 &\\ amp; i \end{bmatrix}= T^2, \qquad X=\begin{bmatrix} 0 & 1 \\ 1& 0 \end{bmatrix}= HT^4H,$$

$$ Y =\begin{bmatrix} 0 & -i i \\& 0 \end{bmatrix}=T^2HT^4 HT^6, \qquad Z=\begin{bmatrix}1& 0\\ 0&-1 \end{bmatrix}=T^4. $$

Itt az X$, $Y$ és $Z$ műveleteket $különösen gyakran használják, és alkotójuk, Wolfgang Pauli után Pauli operátornak nevezik őket. A nem Clifford-kapuval (a T-kapuval$) együtt ezek a $műveletek úgy állíthatók össze, hogy egyetlen qubiten hozzávetőlegesen bármilyen egységes átalakítást lehessen végezni.

Míg az előző a legnépszerűbb primitív kapuk a verem logikai szintjén végzett műveletek leírásához (a logikai szintet a kvantum-algoritmus szintjének tekintik), gyakran kényelmes, ha az algoritmikus szinten kevésbé alapműveleteket, például a függvények leírási szintjéhez közelebbi műveleteket érdemes figyelembe venni. Szerencsére vannak olyan módszerek is, Q# amelyekkel magasabb szintű unitáriusokat lehet implementálni, amelyek lehetővé teszik a magas szintű algoritmusok implementálását anélkül, hogy mindent explicit módon szét kellene bontani a Clifford és $a T-gates$ felé.

A legegyszerűbb ilyen primitív az egyetlen qubit-rotáció. Általában három egy qubites rotációt kell figyelembe venni: $R_x$, $R_y$ és $R_z$. A forgatási $R_x(\theta)$ műveletének vizualizációjához például képzelje el, hogy a jobb hüvelykujja a Bloch-gömb x$ tengelyének $irányába mutat, és a kezével a vektort \theta/2$ radián szögben $forgatja. A 2$ zavaró tényező $abból a tényből ered, hogy az ortogonális vektorok $180^\circ$ egymástól a Bloch-gömbön ábrázolva, de valójában $geometriailag 90^\körfoknyi$ távolságra vannak egymástól. A megfelelő unitáris mátrixok a következők:

\begin{igazítás*}& R_z(\theta) = e^{-i\theta Z/2}=\begin{bmatrix} e^{-i\theta/2&}amp; 0 0\\& amp; e^{i\theta/2\end{bmatrix}}, \\& R_x(\theta) e^{-i\theta X/2=} HR_z(\theta)H =\begin{bmatrix} \cos(\theta/2) & -i\sin(\theta/2)\\ -i\sin(\theta/2) & \cos(\theta/2) \end{bmatrix}, \\& = R_y(\theta) e^-i\theta Y/2=} SHR_z(\theta)HS^\begin{bmatrix}\dagger= \cos(\theta/2) & -\sin(\theta/2)\\ \sin(\theta/2) & \cos(\theta/2) \end{bmatrix}.{= \end{Igazítása*}

Ahogy a három forgatás kombinálható, hogy tetszőleges forgatást hajtsunk végre három dimenzióban, a Bloch-gömb ábrázolásából látható, hogy bármely unitáris mátrix három forgatás sorozataként is írható. Pontosabban, minden unitáris mátrix $U$ létezik $\alpha,\beta,\gamma,\delta$ így $U= e^{i\alpha} R_x(\beta)R_z(\gamma)R_x(\delta)$. Így $R_z(\theta)$ és $H$ is létrehoz egy univerzális kapukészletet, bár nem különálló készlet, mert $a \theta$ bármilyen értéket vehet fel. Ezért, és a kvantumszimulációs alkalmazások miatt az ilyen folyamatos kapuk elengedhetetlenek a kvantumszámításhoz, különösen a kvantumalgoritmusok tervezési szintjén. A hibatűrő hardver implementációja érdekében végső soron különálló kapusorozatokra lesznek lefordítva, amelyek szorosan megközelítik ezeket a rotációkat.

Következő lépések