Note
Access to this page requires authorization. You can try signing in or changing directories.
Access to this page requires authorization. You can try changing directories.
Les deux précédents billets de notre série de rentrée nous ont permis d’introduire le cas d’usage et de présenter dans ce contexte les axes d’amélioration d’une approche avec du #MachineLearning, nos expérimentations Azure ML réalisées pour la circonstance et les résultats obtenus dans ce contexte.
Pour continuer dans cette dynamique, il nous paraitrait à présent intéressant de considérer un autre aspect du travail du scientifique des données (Data Scientist) : celui de faire des choix ou arbitrages quant aux choix des possibles en fonction du besoin et des attentes exprimées.
Dans cette optique, le présent billet est consacré aux différents choix et arbitrages réalisés lors de la construction de nos expérimentations Azure Machine Learning (Azure ML).
Après un rappel sur le partitionnement des données (clustering), nous vous présenterons les 2 types de problématiques couramment rencontrées lorsqu’on souhaite faire un clustering :
- Celle concernant le choix de la distance comme mesure de la dissimilitude.
- Et celle concernant le choix de l’algorithme de clustering à appliquer.
Un bref rappel sur le clustering
Le but du clustering est ici de regrouper les tags en groupes homogènes. Dans le domaine de l’apprentissage automatique, on se situe ici dans l’apprentissage non supervisé. On souhaite en effet classer les tags sans disposer d’un ensemble d’entrainement (avec données labellisées) et on ne connait pas à priori les différentes classes auxquelles seront affiliés les tags.
Le clustering consiste à regrouper les tags en groupes homogènes appelés classes ou clusters, de sorte que les tags à l’intérieur d’une même classe soient similaires, et les tags appartenant à deux classes différentes soient différents.
Le clustering se fonde sur l’égalité suivante :
Concrètement, les algorithmes de clustering construisent des classes de tags de manière à :
- Minimiser l’inertie intra-classe (la distance entre les éléments d’une même classe est minimale)
- Maximiser l’inertie interclasse (La distance entre chaque classe est maximale)
Rappelez-vous le billet Un peu de théorie pour l’apprentissage non supervisé :
On utilise beaucoup le clustering dans la fouille de textes (Text Mining).
Il s’agit alors d’utiliser les tags au sein des articles pour faire des regroupements d’articles. Pour le sujet des « Trending Topics », nous avons choisi de nous inspirer de ces méthodes : il ne s’agit plus d’utiliser les tags pour classer les articles mais d’utiliser les tags pour classer les tags eux-mêmes.
Pour réaliser un clustering, il nous faut d’abord choisir la distance qui va nous servir à mesurer la dissimilitude entre 2 tags. L’idée est la suivante : plus la distance est faible plus les tags sont similaires et susceptibles d’appartenir au même cluster.
Problématique 1 : Quelle formule de la distance convient le mieux ?
Voici quelques distances :
- Distance euclidienne : longueur qui sépare à vol d’oiseaux 2 points dans l’espace.
- Distance de Manhattan : Le nom de cette distance est inspiré du fameux quartier de New York, constitué de nombreux gratte-ciels. Il est impossible de se rendre d’un point à un autre à vol d’oiseau, il faut donc contourner les bâtiments.
Dans le même genre d’approche, on a les distances de Minkowski, de Sebestyen, de Mahalanobis, etc.
- Distance de Hamming : lorsque les coordonnées sont discrètes, cette distance nous donne le nombre de fois où les vecteurs diffèrent. En utilisant la matrice de contingence
 ,
,
- Distance cosinus : permet de calculer la similarité entre deux vecteurs à plusieurs dimensions en déterminant le cosinus de l'angle entre eux.
La distance cosinus est toujours comprise entre -1 et +1 et peut être reliée intuitivement avec la notion de corrélation de la manière suivante. Plus deux tags sont similaires et plus ils auront tendance à apparaitre ensemble dans des articles. Cela se traduit géométriquement par des vecteurs "colinéaires", c'est à dire par un angle faible entre eux et donc un cosinus proche de +1 ou -1. Inversement, deux tags non similaires auront tendance à ne pas apparaitre au sein des articles. Graphiquement, leurs vecteurs sont "orthogonaux" et leur cosinus sera proche de 0.
- Distance de cluster : il s’agit d’une variante de la distance cosinus qui est asymétrique : si i et similaire à j cela ne veut pas dire que j est similaire à i
- Distance de Jaccard : elle est particulièrement efficace pour détecter les doublons.
De toutes ces approches et formules de la distance, il nous a semblé plus judicieux d’utiliser la distance cosinus. Elle présente en effet l’avantage d’être simple et rapide à calculer. De plus, elle reflète bien notre vision géométrique de la dissimilitude entre les tags.
Comme nous l’avons expliqué dans le précédent billet, les distances euclidienne, de Manhattan etc. ne sont pas satisfaisantes ici car les coordonnées des points sont les cooccurrences des tags dans les articles : c’est la corrélation entre les vecteurs qu’on souhaite donc mesurer. Nous ne voulons pas non plus d’une distance asymétrique et nous trouvons que la distance de Jaccard est plus intéressante lorsque les attributs sont de type caractère. Ce qui n’est pas le cas ici.
Nous avons donc préféré utiliser la distance cosinus qui selon nous, est la plus adéquate pour atteindre nos objectifs.
Problématique 2 : Quelle méthode de clustering adopter ?
On peut distinguer 3 familles de modèles de clustering :
- Clustering hiérarchique
- Clustering par partitionnement
- Clustering par modélisation statistique
Pour chacun de ces modèles, on trouve une multitude d’algorithmes.
Principe du clustering Hiérarchique Ascendant (CHA)
Le principe de ce clustering est le suivant : chaque point ou cluster est progressivement "absorbé" par le cluster le plus proche.
Cet algorithme nécessite de choisir 2 métriques :
- La distance entre les points (métrique) : distance euclidienne, distance de Manhattan, etc.
- La distance entre les clusters (ultra-métrique) : il y en a 4 selon la méthode d’agglomération qu’on souhaite appliquer :
- Le saut minimum : retient le minimum des distances entre individus de CI et CJ (simple, mais a tendance à tout agglomérer de proche en proche).
- Le saut maximum : retient le maximum des distances entre individus de CI et CJ.
- Le lien moyen : consiste à calculer la moyenne des distances entre les individus de CI et CJ.
- La distance de Ward : vise à maximiser l'inertie interclasse (produit des clusters plus compacts).
Voici le fonctionnement de l’algorithme :
- Initialisation :
- Chaque individu est assimilé à un cluster,
- On calcule la matrice de ressemblance M entre chaque couple de clusters
- Pour chaque itération :
- On sélectionne dans M des deux clusters les plus proches CI et CJ selon l’ultra métrique choisie
- On fusionne CI et CJ pour former un cluster CG, les points de CI et CJ sont alors assimilés à leur centre
- On met à jour M en calculant la ressemblance entre CG et les clusters existants
- Jusqu’à la fusion des 2 derniers clusters
La représentation des agglomérations successives se fait via un dendrogramme :
Avantages et inconvénients de cet algorithme dans le contexte des « Trending Topics » :
- Il dépend de la métrique et de l’ultra métrique choisie.
- Il est difficile de savoir à quelle hauteur couper le dendrogramme pour déterminer les clusters.
- Mais par contre il est déterministe : une fois la métrique et l’ultra-métrique choisie, on retombe à chaque itération sur le même résultat.
Il existe également des variantes du CHA comme les algorithmes CHAMELEON ou CURE.
Le Clustering Hiérarchique Descendant ou CHD, lui, adopte une démarche inverse : il sélectionne le cluster le moins cohérent puis le subdivise en sous-clusters. Mais la subdivision requiert parfois un CHA ce qui rend cette approche plus complexe et moins intéressante que la précédente dans notre contexte.
Principe du clustering par partitionnement
L’approche de ce type de clustering est la suivante : à partir de N points. L’objectif est de répartir ces N points en K < N clusters. Pour atteindre de manière exacte cet objectif, il faudrait :
- Construire toutes les partitions possibles de l’ensemble des N points en K classes
- Evaluer chacune de ces partitions
- Choisir la meilleure
Le problème est que le nombre de partitions possibles augmente exponentiellement en fonction de K :
Ce traitement devient donc très vite très couteux en temps.
Les algorithmes de clustering par partitionnement ont été créés de manière à pallier à ce problème en adoptant une approche plus approximative ou heuristique. L’idée n’est pas de trouver la partition optimale mais une bonne partition avoir à calculer toutes les partitions possibles. Comment donc la trouver ?
On se fonde sur l’égalité donnée précédemment :
Or, l’inertie totale des points étant fixée, maximiser l’inertie Inter-cluster revient à minimiser l’inertie Intra-cluster :
L’un des algorithmes de partitionnement les plus répandus est celui des K-Moyennes.
Il nécessite de choisir au préalable :
- La distance entre les points (métrique) : distance euclidienne, distance de Manhattan, etc.
- Le nombre de clusters K
Voici le fonctionnement de l’algorithme :
- Initialisation :
- On choisit aléatoirement K points qui constitueront les centres initiaux des K clusters
- Pour chaque itération :
- On calcule les distances entre chaque point et les centres de gravité des K clusters
- On affecte chacun de ces points à son cluster le plus proche
- On recalcule le centre de chaque cluster
On peut obtenir une représentation graphique des résultats :
Avantages et inconvénients de cet algorithme dans le contexte des Trending Topics :
- Comme souligné précédemment, l’algorithme minimise l’inertie Intra-cluster. Le but est de réitérer l’algorithme tant que cette inertie diminue et de s’arrêter ensuite. Cet algorithme peut ainsi amener à converger vers un minimum local et non le minimum global.
- De plus, les centres initiaux des clusters sont déterminés de manière aléatoire.
- Conséquence des deux précédents points, des initialisations différentes peuvent donner des partitions différentes. Il n’y a pas de déterminisme.
- Cet algorithme est basé sur le calcul de la moyenne des classes et ne prend en compte leur dispersion. Ce qui peut être intéressant.
- Le nombre de clusters est à définir à priori, ce qui n’est pas toujours évident. Dans notre cas, le nombre de clusters a été donné par News Republic. Cependant, il est possible de le calculer automatiquement en ajoutant des contraintes sur les clusters (ex : pas plus de 50 tags par clusters).
Il existe de nombreuses variantes de l’algorithme des K-Moyennes. Pour remédier au problème des minimums locaux, il existe une forme forte du K-Moyennes qui consiste à lancer plusieurs fois consécutives l’algorithme et de grouper ensembles les tags qui apparaitraient à chaque fois dans les mêmes clusters. A l’inverse, dans sa forme floue, le K-Moyennes permettrait à un même tag d’appartenir à plusieurs clusters en même temps. Pour prendre en considération la dispersion des tags au sein des clusters, il est possible d’utiliser par exemple la médiane (K-Medians) etc.
Principe du clustering par modélisation statistique
Il s’agit encore une fois d’une approche différente. Il s’agit d’identifier parmi l’ensemble des points ceux qui appartiennent à la même distribution (loi normale, de poisson, uniforme, etc.), de les grouper ainsi en fonction.
Le fait est qu’on ne connait ni les paramètres des distributions, ni les groupes de points appartenant aux même distributions. L’algorithme EM alterne entre calcul des probabilités à postériori d’appartenance à une classe et estimation des paramètres du modèle de mélange (Expectation- Maximisation de la vraisemblance). L’algorithme identifie ainsi lui-même le nombre de distributions et donc de clusters et réalise l’affection des points aux clusters.
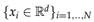 Pour revenir au principe de base et expliquer l’utilité des modèles de mélange pour le clustering, nous vous proposons de réfléchir à l’aide d’un exemple.
Pour revenir au principe de base et expliquer l’utilité des modèles de mélange pour le clustering, nous vous proposons de réfléchir à l’aide d’un exemple.
On considère N points formant deux classes C1 et C2.
On souhaite alors trouver le modèle statistique des données. On peut constater graphiquement qu’il nous faut dans ce cas 2 distributions de Gauss pour modéliser nos données.
- Dans la classe 1 (en rouge), les données suivent une loi normale multidimensionnelle N (X; μ1, Σ1) où X désigne une variable aléatoire telle que μ désigne sa moyenne et Σ sa matrice de variance-covariance.
- Dans la classe 2 (en bleu), les données suivent une loi normale N (X; μ2, Σ2) où X désigne une variable aléatoire.
La densité de X est alors donnée par :
f (X) = f (X∩Z = 1) + f (X∩Z = 2) où Z est une variable aléatoire cachée indiquant la classe du point X.
f (X) = f (X|Z = 1)P(Z = 1) + f (X|Z = 2)P(Z = 2) par formule de Bayes,
f (X|Z = 1) ≡ N (X; μ1, Σ1) et f (X|Z = 2) ≡ N (X; μ2, Σ2)
f(X) = π1f(X|Z = 1) + π2f(X|Z = 2) où π1 et π2 désignent respectivement les probabilités a priori que X appartienne à la classe C1 et C2 et soient tels que π1 + π2 = 1.
f(X) est entièrement déterminé par la connaissance de πj, μj, Σj, j ∈ {1, 2}.On l’appelle modèle de mélange de densités. Par exemple, un modèle de mélange gaussien est de la forme :
f(X) = π1N (X; μ1, Σ1) + π2N (X; μ2, Σ2)
L’idée est alors premièrement de déterminer le modèle de mélange.
Pour cela, on estime les paramètres du modèle (ici π1, π2, μ1, μ2, Σ1, Σ2) par maximisation de la vraisemblance (ou de la log-vraisemblance). Maintenant qu’on connait les probabilités a priori πj et les lois conditionnelles f(X|Z = j), j ∈ {1, 2}, la formule de Bayes nous permet alors d’en déduire les probabilités a posteriori d’appartenance du point X = x à C1 et C2 soit P(Z = 1|X = x) et P(Z = 2|X = x). Ces probabilités étant connues, on affecte le point X=x à la classe de plus grande probabilité conditionnelle.
Dans ce sens, l’algorithme EM est une approche itérative alternant calcul des P(zi = 1|xi), i ∈ {1..K}, et calcul des paramètres (Expectation - Maximisation)
Voici le fonctionnement de l’algorithme :
- Initialisation :
- On fixe les paramètres π1 et π2 tels que π1 + π2 = 1
- On fixe ensuite les paramètres μ1, Σ1, μ2, Σ2
- Initialisation des clusters (par l’utilisation de K-Moyennes par exemple)
- Pour chaque itération :
- Etape E (Expectation) : on calcule les probabilités a posteriori P(zi = 1|xi), i ∈ {1..K}
- Etape M (Maximisation) : on calcule les paramètres
- Jusqu’à convergence
- Après convergence : On dispose des paramètres. On affecte le point xi au cluster Cj de plus grande probabilité conditionnelle
On peut obtenir une représentation graphique des résultats :
Avantages et inconvénients de cet algorithme dans le contexte des « Trending Topics » :
- Cet algorithme présente l’avantage de déterminer lui-même le nombre de clusters.
- On a cependant une convergence vers un extremum local uniquement.
- L’initialisation se fait de manière aléatoire ou en utilisant des résultats a priori (comme l’utilisation de K-Moyennes).
- Des initialisations différentes peuvent donner des paramètres différents.
Une variante de de l’algorithme EM est l’algorithme CEM. Dans l’algorithme EM, la classification se fait après convergence des estimations. L’algorithme CEM, lui, réalise la classification à chaque itération, entre le calcul des probabilités à postériori et le calcul des paramètres du modèle de mélange. L’avantage est qu’on obtient directement les clusters à la fin de l’algorithme.
Les 2 approches de clustering testées et leurs résultats
Après avoir ainsi fait le tour des possibilités en termes de clustering sur les tags, nous avons dû faire des choix :
Vu l’importance du nombre de tags à traiter (environ 46 000), nous avons décidé de ne pas utiliser le CHA.
Nous avons alors simulé 3 distributions et vu que l’EM permettait parfois de surperformer le K-Moyennes comme on peut le voir ici sur ses sorties R :
Algorithme EM
Algorithme des K-Moyennes
Nous avons ainsi préféré nous focaliser sur le K-Moyennes et l’EM. Nous avons ainsi testé ces 2 algorithmes sur R, joué sur les paramètres, et en voici les nuages de points obtenus sur Azure ML :
Algorithme EM
Algorithme des K-Moyennes
En guise de conclusion pour cette troisième partie
On voit ici qu’avec l’EM, certains tags réapparaissent plusieurs fois dans les clusters. Par exemple, le tag « Football » appartient à 3 clusters différents, clusters qui au final pourraient être fusionnés en un seul. De plus, l’utilisation de cet algorithme est ici plus couteuse en termes de temps d’exécution.
De l’autre côté, les clusters obtenus avec les K-Moyennes sont totalement cohérents et donnent bien 8 groupes de tags répartis en thèmes facilement identifiables ici : le sport, l’économie, l’informatique, le cinéma américain, etc.
Nous avons donc préféré réaliser le clustering des tags à l’aide de l’algorithme des K-Moyennes.
Dans la continuité de ce billet, le prochain billet sera dédié aux réflexions faites autour d’une autre problématique : le choix de la méthode de calcul de la tendance. Puisque nous recherchons à identifier les « Trending Topics », il nous faut savoir ce qui fait qu’un topic est considéré comme « trending ».






















